Question

【题目】如图，D为⊙O上一点，点C在直径BA的延长线上，∠CDA=∠CBD．

（1）求证：CD是⊙O的切线；
（2）过点B作⊙O的切线交CD的延长线于点E，若AB=6，tan∠CDA= ，依题意补全图形并求DE的长．

Answer 1

【答案】
（1）证明：连OD，OE，如图1所示，

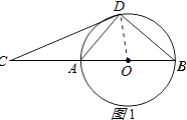
∵AB为直径，

∴∠ADB=90°，

即∠ADO+∠BDO=90°，

又∵∠CDA=∠CBD，

而∠CBD=∠BDO，

∴∠BDO=∠CDA，

∴∠CDA+∠ADO=90°，

即∠CDO=90°，

∴CD⊥OD，

∴CD是⊙O的切线

（2）解：如图2所示：

∵EB为⊙O的切线，

∴ED=EB，OE⊥DB，

∴∠ABD+∠DBE=90°，∠OEB+∠DBE=90°，

∴∠ABD=∠OEB，

∴∠CDA=∠OEB．

而tan∠CDA= ，

∴tan∠OEB= = ，

∵Rt△CDO∽Rt△CBE，

∴ = ，

∴CD= ×6=4，

在Rt△CBE中，设BE=x，

∴（x+4）2=x2+62，

解得：x= ．

即BE的长为 ，

∴DE=BE= ．

【解析】（1）连OD，OE.由AB为直径可得出∠ADO+∠BDO=90°，再根据圆周角定理和已知可得到∠CDA+∠ADO=90°，进而可证出结论；
（2）由切线的性质和已知可得到∠CDA=∠OEB，进而可得，再由Rt△CDO∽Rt△CBE可求出CD的长，在Rt△CBE中利用勾股定理可求出BE的长，即可得到DE的长.
【考点精析】本题主要考查了相似三角形的性质和锐角三角函数的定义的相关知识点，需要掌握对应角相等，对应边成比例的两个三角形叫做相似三角形；锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数才能正确解答此题．