题目内容
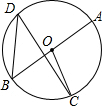
如图，在⊙O中，弦AC⊥BC，若AC=8cm，BC=6cm，则⊙O的半径等于______cm，AC的弦心距等于______cm．
连接AB，OC，过O点作OD⊥AC，D为垂足，如图，
∵弦AC⊥BC，即∠ACB=90°，
∴AB为⊙O的直径，并且AB2=AC2+BC2，
而AC=8cm，BC=6cm，
∴AB=
=10（cm），即OA=5cm．
∵OD⊥AC，
∴AD=CD，
∴OD为△ABC的中位线，
∴OD=
BC=
×6=3（cm）．
故答案为5，3．
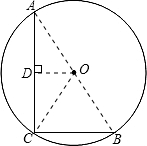
∵弦AC⊥BC，即∠ACB=90°，
∴AB为⊙O的直径，并且AB2=AC2+BC2，
而AC=8cm，BC=6cm，
∴AB=
| 82+62 |
∵OD⊥AC，
∴AD=CD，
∴OD为△ABC的中位线，
∴OD=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为5，3．
练习册系列答案
相关题目
