题目内容
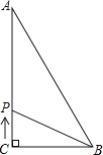
【题目】如图,△ABC中,∠C=90°,AC=12,BC=9,AB=15,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒3个单位,设运动的时间为t秒.
(1)当t=______时,CP把△ABC的面积分成相等的两部分;
(2)当t=5时,CP把△ABC分成的两部分面积之比是S△APC:S△BPC=______
(3)当t=______时,△BPC的面积为18.

【答案】(1)6.5;(2)1:4;(3)![]() 或
或![]() .
.
【解析】
(1)根据中线的性质可知,点P在AB中点,CP把△ABC的面积分成相等的两部分,进而求解即可;
(2)求出当![]() 时,
时,![]() 与
与![]() 的长,再根据等高的三角形面积比等于底边的比求解即可;
的长,再根据等高的三角形面积比等于底边的比求解即可;
(3)分两种情况:①当P在AC上时;②当P在AB上时.
(1)当点P在AB中点时,CP把△ABC的面积分成相等的两部分,此时
∵点P在AB中点
∴![]()
∴CA+AP=12+7.5=19.5(cm),
∴3t=19.5,
解得t=6.5.
故当t=6.5时,CP把△ABC的面积分成相等的两部分;
(2)5×3=15,
AP=15-12=3,
BP=15-3=12,
则S△APC:S△BPC=3:12=1:4;
(3)分两种情况:
①当P在AC上时,
∵△BCP的面积=18,
∴![]() ×9×CP=18,
×9×CP=18,
∴CP=4,
∴3t=4,
∴t=![]() ;
;
②当P在AB上时,
∵△BCP的面积=18,△ABC面积=![]() ,
,
∴![]()
∴3t=12+15×![]() =22,
=22,
解得t=![]() .
.
故t=![]() 或
或![]() 秒时,△BCP的面积为18.
秒时,△BCP的面积为18.
故答案为: ![]() 或
或![]() .
.

【题目】学校为了从李飞与刘亮中选取一人参加市射击比赛,现将他们某次射击训练的成绩绘制了如下图所示的折线统计图:
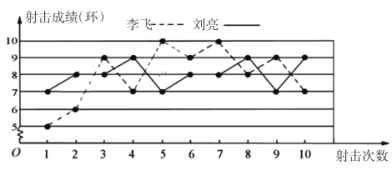
(1)请根据折线统计图中提供的信息填写下表:
平均数 | 中位 | 众数 | |
李飞 | 8 | ||
刘亮 | 8 | 8 |
(2)请计算李飞与刘亮射击训练的成绩的方差.(方差公式:![]() )
)
(3)从折线统计图上分析李飞与刘亮的射击成绩走势和稳定性,派谁去参加射击比赛更合适.