题目内容
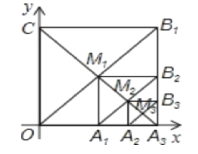
【题目】如图：在正方形网格中有一个△ABC，按要求进行下列作图（只能借助于网格）：
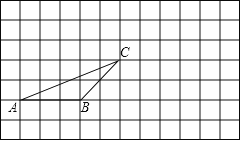
（1）画出△ABC中BC边上的高AD；
（2）画出先将△ABC向右平移6格，再向上平移3格后的△A1B1C1；
（3）若格点△PAB与格点△PBC的面积相等，则这样的点P共______个.
【答案】(1)详见解析;(2)详见解析;(3)4
【解析】
（1）根据网格特点和正方形的性质画出高AD即可；
（2）利用网格特点和平移的性质画出△A1B1C1即可；
（3）建立直角坐标系，根据点到直线的距离公式列出方程求解即可得到两条直线，找出这两条直线上的格点即可．
（1）如图所示，AD即为所求；
（2）如图所示，△A1B1C1即为所求．
（3）如图，以B为原点，AB所在直线为x轴，过B点与AB垂直的直线为y轴，建立直角坐标系，设
∴
∴
∴直线AB的解析式为y=0，直线BC的解析式为y=x
∵格点△PAB与格点△PBC的面积相等
∴
∴
∴
∴
∴
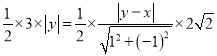
如图，作直线
和直线
，找出这两条直线上的格点即可
这样的点P有4个．
【题目】某经销商从市场得知如下信息：
某品牌空调扇 | 某品牌电风扇 | |
进价（元/台） | 700 | 100 |
售价（元/台） | 900 | 160 |
他现有40000元资金可用来一次性购进该品牌空调扇和电风扇共100台，设该经销商购进空调扇
台，空调扇和电风扇全部销售完后获得利润为
元.
（1）求关于的函数解析式；
（2）利用函数性质，说明该经销商如何进货可获利最大？最大利润是多少元？
【题目】学校组织八年级350名学生参加“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分，为了更好地了解本次大赛的成绩分布情况，随机抽取了其中若干名学生的成绩作为样本进行整理，得到下列不完整的统计图表：
成绩x/分 | 频数 | 频率 |
50≤x<60 | 2 | 0.04 |
60≤x<70 | 6 | 0.12 |
70≤x<80 | 9 | b |
80≤x<90 | a | 0.36 |
90≤x≤100 | 15 | 0.30 |
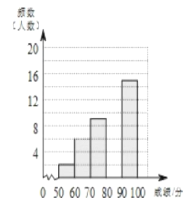
请根据所给信息，解答下列问题：
（1）求a和b的值；
（2）请补全频数分布直方图。
