题目内容
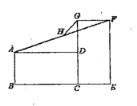
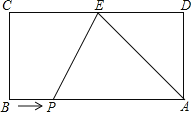
【题目】如图,已知矩形ABCD,AB=8,AD=4,E为CD边上一点,CE=5,P点从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE,设点P运动的时间为t秒,则当t的值为______时,∠PAE为等腰三角形?
【答案】3或2或![]() .
.
【解析】
根据矩形的性质求出∠D=90°,AB=CD=8,求出DE后根据勾股定理求出AE;过E作EM⊥AB于M,过P作PQ⊥CD于Q,求出AM=DE=3,当EP=EA时,AP=2DE=6,即可求出t;当AP=AE=5时,求出BP=3,即可求出t;当PE=PA时,则x2=(x-3)2+42,求出x,即可求出t.
∵四边形ABCD是长方形,
∴∠D=90°,AB=CD=8,
∵CE=5,
∴DE=3,
在Rt△ADE中,∠D=90°,AD=4,DE=3,由勾股定理得:AE=![]() =5;
=5;
过E作EM⊥AB于M,过P作PQ⊥CD于Q,
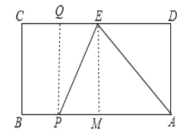
则AM=DE=3,
若△PAE是等腰三角形,则有三种可能:
当EP=EA时,AP=2DE=6,
所以t=![]() =2;
=2;
当AP=AE=5时,BP=85=3,
所以t=3÷1=3;
当PE=PA时,设PA=PE=x,BP=8x,则EQ=5(8x)=x3,
则x2=(x3)2+42,
解得:x=![]() ,
,
则t=(8![]() )÷1=
)÷1=![]() ,
,
综上所述t=3或2或![]() 时,△PAE为等腰三角形.
时,△PAE为等腰三角形.
故答案为:3或2或![]() .
.

【题目】某校为了了解学生对语文、数学、英语、物理四科的喜爱程度(每人只选一科),特对八年级某班进行了调查,并绘制成如下频数和频率统计表和扇形统计图:
科目 | 频数 | 频率 |
语文 |
| 0.5 |
数学 | 12 |
|
英语 | 6 |
|
物理 |
| 0.2 |

(1)求出这次调查的总人数;
(2)求出表中![]() 的值;
的值;
(3)若该校八年级有学生1000人,请你算出喜爱英语的人数,并发表你的看法.
【题目】某经销商从市场得知如下信息:
某品牌空调扇 | 某品牌电风扇 | |
进价(元/台) | 700 | 100 |
售价(元/台) | 900 | 160 |
他现有40000元资金可用来一次性购进该品牌空调扇和电风扇共100台,设该经销商购进空调扇![]() 台,空调扇和电风扇全部销售完后获得利润为
台,空调扇和电风扇全部销售完后获得利润为![]() 元.
元.
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)利用函数性质,说明该经销商如何进货可获利最大?最大利润是多少元?