题目内容
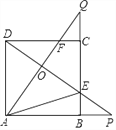
【题目】如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP 交于点O,并分别与边CD,BC 交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=0E![]() OP;③
OP;③![]() ;④当BP=1时,
;④当BP=1时,![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】由四边形ABCD是正方形,得到AD=BC,∠DAB=∠ABC=90°,继而可证明△DAP≌△ABQ,根据全等三角形的性质得到∠P=∠Q,根据余角的性质得到AQ⊥DP;故①正确;证明△DAO∽△APO,根据相似三角形的性质得到AO2=ODOP,由OD≠OE,得到OA2≠OEOP;故②错误;根据全等三角形的性质得到CF=BE,DF=CE,于是得到S△ADF-S△DFO=S△DCE-S△DOF,即S△AOD=S四边形OECF;故③正确;根据相似三角形的性质得到BE=![]() ,求得QE=
,求得QE=![]() ,QO=
,QO=![]() ,OE=
,OE=![]() ,由三角函数的定义即可得到结论.
,由三角函数的定义即可得到结论.
∵四边形ABCD是正方形,
∴AD=BC,∠DAB=∠ABC=90°,
∵BP=CQ,
∴AP=BQ,
在△DAP与△ABQ中,
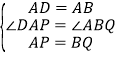 ,
,
∴△DAP≌△ABQ,
∴∠P=∠Q,
∵∠Q+∠QAB=90°,
∴∠P+∠QAB=90°,
∴∠AOP=90°,
∴AQ⊥DP,故①正确;
∵∠DOA=∠AOP=90°,∠ADO+∠P=∠ADO+∠DAO=90°,
∴∠DAO=∠P,
∴△DAO∽△APO,
∴![]() ,
,
∴AO2=ODOP,
∵AE>AB,
∴AE>AD,
∴OD≠OE,
∴OA2≠OEOP;故②错误;
在△CQF与△BPE中,
 ,
,
∴△CQF≌△BPE,
∴CF=BE,
∴DF=CE,
在△ADF与△DCE中,
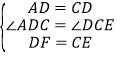 ,
,
∴△ADF≌△DCE,
∴S△ADF-S△DFO=S△DCE-S△DOF,
即S△AOD=S四边形OECF,故③正确;
∵BP=1,AB=3,
∴AP=4,
∵△PBE∽△PAD,
∴![]() ,
,
∴BE=![]() ,∴QE=
,∴QE=![]() ,
,
∵△QOE∽△PAD,
∴![]() ,
,
∴QO=![]() ,OE=
,OE=![]() ,
,
∴AO=5-QO=![]() ,
,
∴tan∠OAE=![]() ,故④错误,
,故④错误,
故选B.

【题目】我国男性的体质系数计算公式是:m=![]() ×100%,其中W表示体重(单位:kg),H表示身高(单位:cm).通过计算出的体质系数m对体质进行评价.具体评价如下表:
×100%,其中W表示体重(单位:kg),H表示身高(单位:cm).通过计算出的体质系数m对体质进行评价.具体评价如下表:
m | <80% | 80%~90% | 90%~110% | 110%~120% | >120% |
评价结果 | 明显消瘦 | 消瘦 | 正常 | 过重 | 肥胖 |
(1)某男生的身高是170cm,体重是75kg,他的体质评价结果是 ;
(2)现从某校九年级学生中随机抽取n名男生进行体质评价,评价结果统计如下:
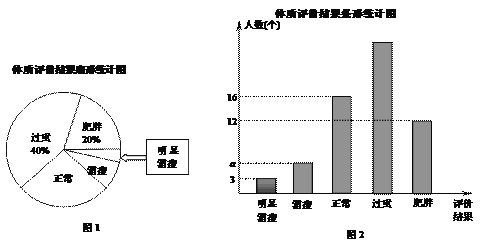
①抽查的学生数n= ;图2中a的值为 ;
②图1中,体质评价结果为“正常”的所在扇形圆心角为 °;
(3)若该校九年级共有男生480人,试估计该校九年级体质评价结果为“过重”或“肥胖”的男生人数.
【题目】某校为了了解学生对语文、数学、英语、物理四科的喜爱程度(每人只选一科),特对八年级某班进行了调查,并绘制成如下频数和频率统计表和扇形统计图:
科目 | 频数 | 频率 |
语文 |
| 0.5 |
数学 | 12 |
|
英语 | 6 |
|
物理 |
| 0.2 |

(1)求出这次调查的总人数;
(2)求出表中![]() 的值;
的值;
(3)若该校八年级有学生1000人,请你算出喜爱英语的人数,并发表你的看法.
【题目】某经销商从市场得知如下信息:
某品牌空调扇 | 某品牌电风扇 | |
进价(元/台) | 700 | 100 |
售价(元/台) | 900 | 160 |
他现有40000元资金可用来一次性购进该品牌空调扇和电风扇共100台,设该经销商购进空调扇![]() 台,空调扇和电风扇全部销售完后获得利润为
台,空调扇和电风扇全部销售完后获得利润为![]() 元.
元.
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)利用函数性质,说明该经销商如何进货可获利最大?最大利润是多少元?