题目内容
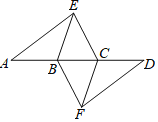
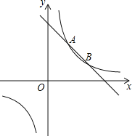
【题目】如图,反比例函数y=![]() 的图象和一次函数的图象交于A、B两点,点A的横坐标和点B的纵坐标都是1.
的图象和一次函数的图象交于A、B两点,点A的横坐标和点B的纵坐标都是1.
(1)在第一象限内,写出关于x的不等式kx+b≥![]() 的解集 ;
的解集 ;
(2)求一次函数的表达式;
(3)若点P(m,n)在反比例函数图象上,且关于y轴对称的点Q恰好落在一次函数的图象上,求m2+n2的值.
【答案】(1)1≤x≤2;(2)y=﹣x+3;(3)13.
【解析】
(1)根据题意得出A、B点的坐标,根据交点即可求得不等式的解集;
(2)根据待定系数法即可求得一次函数的解析式;
(3)求得Q点的坐标,即可求得n=m+3,则P(m.m+3),即可得出m(m+3)=2,m2+n2=m2+(m+3)2=2m2+6m+9=2(m2+3m)+9=13.
解:(1)∵反比例函数y=![]() 的图象和一次函数的图象交于A、B两点,点A的横坐标和点B的纵坐标都是1,
的图象和一次函数的图象交于A、B两点,点A的横坐标和点B的纵坐标都是1,
∴A(1,2),B(2,1),
∴在第一象限内,不等式kx+b≥![]() 的解集为1≤x≤2,
的解集为1≤x≤2,
故答案为1≤x≤2;
(2)设一次函数的解析式为y=kx+b,
∵经过A(1,2),B(2,1)点,
∴![]() ,解得
,解得![]() ,
,
∴一次函数的解析式为y=﹣x+3;
(3)∵点P(m,n),
∴Q(﹣m,n),
∵点P在反比例函数图象上,
∴mn=2
∵点Q恰好落在一次函数的图象上,
∴n=m+3,
∴m(m+3)=2,
∴m2+3m=2,
∴m2+n2=m2+(m+3)2=2m2+6m+9=2(m2+3m)+9=2×2+9=13.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目