Question

【题目】如图，在Rt△ABC中，∠ACB=90°，∠A=30°，BC=2，点D是边AB上的动点，将△ACD沿CD所在的直线折叠至△CDA的位置，CA'交AB于点E．若△A'ED为直角三角形，则AD的长为______．

Answer 1

【答案】3﹣或2

【解析】

分两种情况:情况一：如图一所示，当∠A'DE=90°时；

情况二：如图二所示，当∠A'ED=90°时.

解：如图，当∠A'DE=90°时，△A'ED为直角三角形，

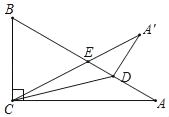
∵∠A'=∠A=30°，

∴∠A'ED=60°=∠BEC=∠B，

∴△BEC是等边三角形，

∴BE=BC=2，

又∵Rt△ABC中，AB=2BC=4，

∴AE=2，

设AD=A'D=x，则DE=2﹣x，

∵Rt△A'DE中，A'D=DE，

∴x=（2﹣x），

解得x=3﹣，

即AD的长为3﹣；

如图，当∠A'ED=90°时，△A'ED为直角三角形，

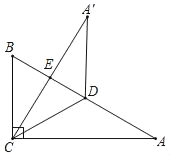
此时∠BEC=90°，∠B=60°，

∴∠BCE=30°，

∴BE=BC=1，

又∵Rt△ABC中，AB=2BC=4，

∴AE=4﹣1=3，

∴DE=3﹣x，

设AD=A'D=x，则

Rt△A'DE中，A'D=2DE，即x=2（3﹣x），

解得x=2，

即AD的长为2；

综上所述，即AD的长为3﹣或2．

故答案为：3﹣或2．