��Ŀ����
����Ŀ������һ�ֲ�Ʒ�����Ƚ����ϼ��ȴﵽ60 �����ٽ��в�������ò����¶�Ϊy���������Ӽ��ȿ�ʼ�����ʱ��Ϊx��min�������˽⣬���ò��ϼ���ʱ���¶�y��ʱ��x��һ�κ�����ϵ��ֹͣ���Ƚ��в���ʱ���¶�y��ʱ��x�ɷ�������ϵ����ͼ������֪�ò����ڲ�������ǰ���¶�Ϊ15 ��������5���Ӻ��¶ȴﵽ60 ����
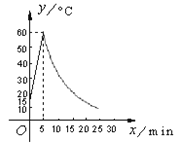
��1���ֱ���������ϼ��Ⱥ�ֹͣ���Ƚ��в���ʱ��y��x�ĺ�����ϵʽ��
��2�����ݹ���Ҫ�����ϵ��¶ȵ���15 ��ʱ����ֹͣ��������ô�ӿ�ʼ���ȵ�ֹͣ�������������˶���ʱ�䣿
���𰸡���1��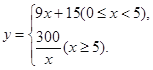 ��2��20����
��2��20����
���������⣺��1�����ϼ���ʱ����y=ax+15��a��0����
�������60=5a+15��
���a=9��
����ϼ���ʱ��y��x�ĺ�����ϵʽΪy=9x+15��0��x��5����
ֹͣ����ʱ����y=��k��0����
�������60=��
���k=300��
��ֹͣ���Ƚ��в���ʱy��x�ĺ�����ϵʽΪy=![]() ��x��5����
��x��5����
��2����y=15����y=![]() ����x=20��
����x=20��
��˴ӿ�ʼ���ȵ�ֹͣ��������������20���ӣ�
�𣺴ӿ�ʼ���ȵ�ֹͣ��������������20���ӣ�

��ϰ��ϵ�д�
 ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д�
�����Ŀ