Question

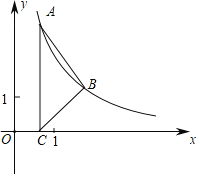
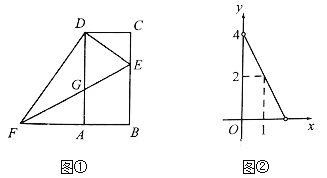
【题目】如图①，四边形是知形，，点是线段上一动点(不与重合)，点是线段延长线上一动点，连接交于点.设，已知与之间的函数关系如图②所示.

（1）求图②中与的函数表达式;

（2）求证:;

（3）是否存在的值，使得是等腰三角形?如果存在，求出的值;如果不存在，说明理由

Answer 1

【答案】（1）y＝﹣2x+4（0＜x＜2）；（2）见解析；（3）存在，x＝或或．

【解析】

（1）利用待定系数法可得y与x的函数表达式；

（2）证明△CDE∽△ADF，得∠ADF＝∠CDE，可得结论；

（3）分三种情况：

①若DE＝DG，则∠DGE＝∠DEG，

②若DE＝EG，如图①，作EH∥CD，交AD于H，

③若DG＝EG，则∠GDE＝∠GED，

分别列方程计算可得结论．

（1）设y＝kx+b，

由图象得：当x＝1时，y＝2，当x＝0时，y＝4，

代入得：，得，

∴y＝﹣2x+4（0＜x＜2）；

（2）∵BE＝x，BC＝2

∴CE＝2﹣x，

∴，

∴，

∵四边形ABCD是矩形，

∴∠C＝∠DAF＝90°，

∴△CDE∽△ADF，

∴∠ADF＝∠CDE，

∴∠ADF+∠EDG＝∠CDE+∠EDG＝90°，

∴DE⊥DF；

（3）假设存在x的值，使得△DEG是等腰三角形，

①若DE＝DG，则∠DGE＝∠DEG，

∵四边形ABCD是矩形，

∴AD∥BC，∠B＝90°，

∴∠DGE＝∠GEB，

∴∠DEG＝∠BEG，

在△DEF和△BEF中，

，

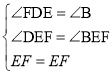∴△DEF≌△BEF（AAS），

∴DE＝BE＝x，CE＝2﹣x，

∴在Rt△CDE中，由勾股定理得：1+（2﹣x）2＝x2，

x＝；

②若DE＝EG，如图①，作EH∥CD，交AD于H，

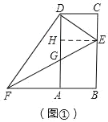
∵AD∥BC，EH∥CD，

∴四边形CDHE是平行四边形，

∴∠C＝90°，

∴四边形CDHE是矩形，

∴EH＝CD＝1，DH＝CE＝2﹣x，EH⊥DG，

∴HG＝DH＝2﹣x，

∴AG＝2x﹣2，

∵EH∥CD，DC∥AB，

∴EH∥AF，

∴△EHG∽△FAG，

∴，

∴，

∴（舍），

③若DG＝EG，则∠GDE＝∠GED，

∵AD∥BC，

∴∠GDE＝∠DEC，

∴∠GED＝∠DEC，

∵∠C＝∠EDF＝90°，

∴△CDE∽△DFE，

∴，

∵△CDE∽△ADF，

∴，

∴，

∴2﹣x＝，x＝，

综上，x＝或或．