题目内容
已知如图,对称轴为直线x=4的抛物线y=ax2+2x与x轴相交于点B、O.
(1)求抛物线的解析式.
(2)连接AB,平移AB所在的直线,使其经过原点O,得到直线l.点P是l上一动点,当△PAB的周长最小时,求点P的坐标.
(3)当△PAB的周长最小时,在直线AB的上方是否存在一点Q,使以A,B,Q为顶点的三角形与△POB相似?若存在,直接写出点Q的坐标;若不存在,说明理由.(规定:点Q的对应顶点不为点O)

(1)求抛物线的解析式.
(2)连接AB,平移AB所在的直线,使其经过原点O,得到直线l.点P是l上一动点,当△PAB的周长最小时,求点P的坐标.
(3)当△PAB的周长最小时,在直线AB的上方是否存在一点Q,使以A,B,Q为顶点的三角形与△POB相似?若存在,直接写出点Q的坐标;若不存在,说明理由.(规定:点Q的对应顶点不为点O)

(1)∵对称轴为直线x=-
=4,
∴a=-
,
∴抛物线解析式为y=-
x2+2x;
(2)∵y=-
x2+2x=-
(x2-8x+16)+4=-
(x-4)2+4,
∴顶点坐标为A(4,4),
令y=0,则-
x2+2x=0,
解得x1=0,x2=8,
∴点B的坐标为(8,0),
设直线AB的解析式为y=kx+b,
则
,
解得
,
所以,直线AB的解析式为y=-x+8,
∵直线l为直线AB平移至经过原点的直线,
∴直线l的解析式为y=-x,
如图,取点A关于直线l的对称点A′,连接A′B交直线l于点P,则△PAB的周长最小,
此时,点A(-4,-4),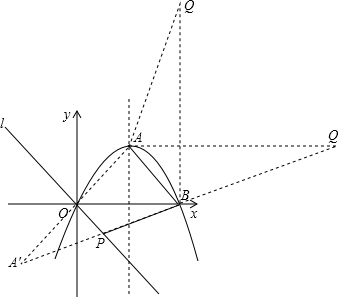
点P为线段A′B的中点,
∵
=2,
=-2,
∴点P的坐标为(2,-2);
(3)∵直线AB的解析式为y=-x+8,
∴直线AB与x轴、对称轴的夹角的锐角为45°,
又∵l∥AB,
∴∠POB=45°,
根据勾股定理,AB=
=4
,
PO=
=2
,
①∠BAQ=∠POB=45°时,∵△POB∽△BAQ,
∴
=
,
即
=
,
解得AQ=16,
∴Q的横坐标为16+4=20,纵坐标为4,
∴点Q的坐标为(20,4);
②∠ABQ=∠POB=45°时,∵△POB∽△ABQ,
∴
=
,
即
=
,
解得BQ=16,
∴点Q的坐标为(8,16),
综上所述,存在点Q(20,4)或(8,16)使以A,B,Q为顶点的三角形与△POB相似.
| 2 |
| 2a |
∴a=-
| 1 |
| 4 |
∴抛物线解析式为y=-
| 1 |
| 4 |
(2)∵y=-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
∴顶点坐标为A(4,4),
令y=0,则-
| 1 |
| 4 |
解得x1=0,x2=8,
∴点B的坐标为(8,0),
设直线AB的解析式为y=kx+b,
则
|
解得
|
所以,直线AB的解析式为y=-x+8,
∵直线l为直线AB平移至经过原点的直线,
∴直线l的解析式为y=-x,
如图,取点A关于直线l的对称点A′,连接A′B交直线l于点P,则△PAB的周长最小,
此时,点A(-4,-4),

点P为线段A′B的中点,
∵
| -4+8 |
| 2 |
| -4+0 |
| 2 |
∴点P的坐标为(2,-2);
(3)∵直线AB的解析式为y=-x+8,
∴直线AB与x轴、对称轴的夹角的锐角为45°,
又∵l∥AB,
∴∠POB=45°,
根据勾股定理,AB=
| 42+(8-4)2 |
| 2 |
PO=
| 22+22 |
| 2 |
①∠BAQ=∠POB=45°时,∵△POB∽△BAQ,
∴
| PO |
| AB |
| OB |
| AQ |
即
2
| ||
4
|
| 8 |
| AQ |
解得AQ=16,
∴Q的横坐标为16+4=20,纵坐标为4,
∴点Q的坐标为(20,4);
②∠ABQ=∠POB=45°时,∵△POB∽△ABQ,
∴
| PO |
| AB |
| OB |
| BQ |
即
2
| ||
4
|
| 8 |
| BQ |
解得BQ=16,
∴点Q的坐标为(8,16),
综上所述,存在点Q(20,4)或(8,16)使以A,B,Q为顶点的三角形与△POB相似.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 重合,点A在x轴上,点B在y轴上
重合,点A在x轴上,点B在y轴上
 ,OB=4,现将Rt△AOB绕着直角顶点O按逆时针方向旋转90°得到△COD,已知一抛物线经过C、D、B三点.
,OB=4,现将Rt△AOB绕着直角顶点O按逆时针方向旋转90°得到△COD,已知一抛物线经过C、D、B三点.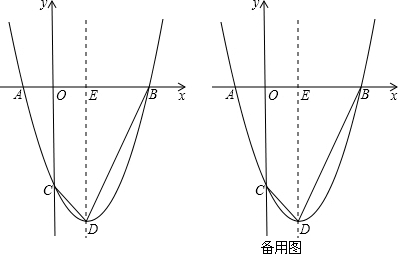
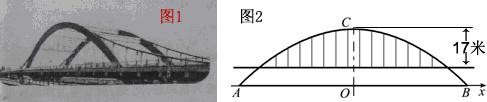

 对称轴与x轴的交点.
对称轴与x轴的交点.