题目内容
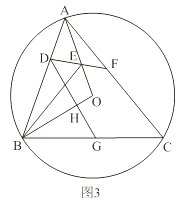
【题目】如图，点P在以AB为直径的半圆内，连接AP、BP，并延长分别交半圆于点C、D，连接AD、BC并延长交于点F，作直线PF，下列说法一定正确的是（ ）
①AC垂直平分BF；②AC平分∠BAF；③FP⊥AB；④BD⊥AF．
A. ①③ B. ①④ C. ②④ D. ③④
【答案】D
【解析】试题分析：①∵AB为直径，∴∠ACB=90°，∴AC垂直BF，但不能得出AC平分BF，故①错误，②如图1，连结CD，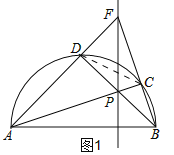
∵AB为直径，∴∠ADB=90°，∴∠BDF=90°，假设AC平分∠BAF成立，则有DC=BC，∴在RT△FDB中，DC=BC=FC，∴AC⊥BF，且平分BF，∴AC垂直BF，但不能得出AC平分BF，与①中的AC垂直BF，但不能得出AC平分BF相矛盾，故②错误，③如图2：
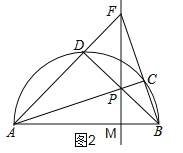
∵AB为直径，∴∠ACB=90°，∠ADB=90°，∴D、P、C、F四点共圆，∴∠CFP和∠CDB都对应
，∴∠CFP=∠CDB，∵∠CDB=∠CAB，∴∠CFP=∠CAB，又∵∠FPC=∠APM，∴△AMP∽△FCP，∠ACF=90°，∴∠AMP=90°，∴FP⊥AB，故③正确，④∵AB为直径，∴∠ADB=90°，∴BD⊥AF．
故④正确，综上所述只有③④正确．
故选D．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目
