Question

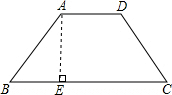
如图，在等腰梯形ABCD中，AB=2，BC=4，∠B=45°，则该梯形的面积是（　　）

A．2 2 -1

B．4- 2

C．8 2 -4

D．4 2 -2

Answer 1

作AE垂直BC于点E
已知AB=2，∠B=45°，根据勾股定理可得BE=AE=

2

AD=BC-2BE=4-2

2

故梯形的面积为：（4-2

2

+4）×

2

×

1

2

=4

2

-2
故选D