题目内容
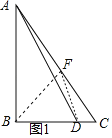
【题目】如图，在△ABC中，AB＝BC，∠B＝90°，点D为直线BC上一个动点（不与B，C重合），连结AD．将线段AD绕点D按顺吋针方向旋转90°得到线段DE，连结EC．
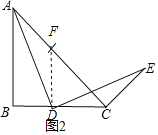
（1）如图1，点D在线段BC上，依题意画图得到图2．
①求证：∠BAD＝∠EDC；
②方方同学通过观察、测量得出结论：在点D运动的过程中，总有∠DCE＝135°．方方的主要思路有以下几个：
思路一：在AB上取一点F使得BF＝BD，要证∠DCE＝135°，只需证△ADF≌△DEC．
思路二：以点D为圆心，DC为半径画弧交AC于点F，要证∠DCE＝135°，只需证△AFD≌△ECD．
思路三：过点E作BC所在直线的垂线段EF，要证∠DCE＝135°，只需证EF＝CF．
……
请你参考井选择其中一个思路，证明∠DCE＝135°；
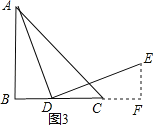
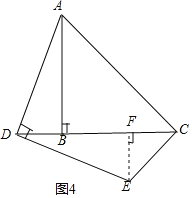
（2）如果点D在线段CB的延长线上运动，利用图3画图分析，∠DCE的度数还是确定的值吗？如果是，请写出∠DCE的度数并说明理由；如果不是，也请说明你的理由．
【答案】（1）①见解析，②见解析；（2）∠DCE＝45°，理由见解析
【解析】
（1）①根据余角的性质得到结论；②证法1：如图1，在AB上取点F，使得BF＝BD，连接DF，根据等腰直角三角形的性质得到∠BFD＝45°，根据全等三角形的性质得到∠DCE＝∠AFD＝135°；证法2：以D为圆心，DC为半径作弧交AC于点F，连接DF，根据全等三角形的性质即可得到结论；证法3：过点E作EF⊥BC交BC的延长线于点F，根据全等三角形的性质即可得到结论；
（2）过E作EF⊥DC于F，根据全等三角形的性质得到DB＝EF，AB＝DF＝BC，根据线段的和差得到FC＝EF，于是得到结论．
解：（1）①证明：∵∠B＝90°，
∴∠BAD+∠BDA＝90°，
∵∠ADE＝90°，点D在线段BC上，
∴∠BAD+∠EDC＝90°，
∴∠BAD＝∠EDC；
②证法1：如图1，在AB上取点F，使得BF＝BD，连接DF，
∵BF＝BD，∠B＝90°，
∴∠BFD＝45°，
∴∠AFD＝135°，
∵BA＝BC，
∴AF＝CD，
在△ADF和△DEC中，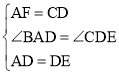
，
∴△ADF≌△DEC，（SAS），
∴∠DCE＝∠AFD＝135°；
证法2：如图2，以D为圆心，DC为半径作弧交AC于点F，连接DF，
∴DC＝DF，∠DFC＝∠DCF，
∵∠B＝90°，AB＝BC，
∴∠ACB＝45°，∠DFC＝45°，
∴∠DFC＝90°，∠AFD＝135°，
∵∠ADE＝∠FDC＝90°，
∴∠ADF＝∠EDC，
在△ADF≌△CDE中，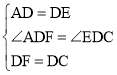
，
∴△ADF≌△CDE，（SAS），
∴∠AFD＝∠DCE＝135°；
证法3：如图3，过点E作EF⊥BC交BC的延长线于点F，
∴∠EFD＝90°，
∵∠B＝90°，
∴∠EFD＝∠B，
在△ABD和△DFE中，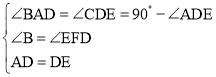
，
∴△ABD≌△DFE，（AAS），
∴AB＝DF，BD＝EF，
∵AB＝BC，
∴BC＝DF，BC﹣DC＝DF﹣DC，
即BD＝CF，
∴EF＝CF，
∵∠EFC＝90°，
∴∠ECF＝45°，∠DCE＝135°；
（2）解：∠DCE＝45°，
理由：如图4，过E作EF⊥DC于F，
∵∠ABD＝90°，
∴∠EDF＝∠DAB＝90°﹣∠ADB，
在△ABD和△DFE中，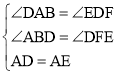
，
∴△ABD≌△DFE，（AAS），
∴DB＝EF，AB＝DF＝BC，
∴BC﹣BF＝DF﹣BF，
即FC＝DB，
∴FC＝EF，
∴∠DCE＝45°．
