题目内容
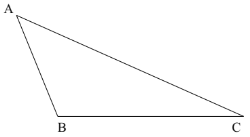
【题目】如图,已知直线y=-2x+12分别与y轴,x轴交于A,B两点,点M在y轴上,以点M为圆心的⊙M与直线AB相切于点D,连接MD.
(1)求证:△ADM∽△AOB.
(2)如果⊙M的半径为2![]() ,请写出点M的坐标,并写出以点
,请写出点M的坐标,并写出以点![]() 为顶点,且过点M的抛物线的函数表达式.
为顶点,且过点M的抛物线的函数表达式.
(3)在(2)的条件下,试问在此抛物线上是否存在点P,使以P,A,M三点为顶点的三角形与△AOB相似?如果存在,请求出所有符合条件的点P的坐标;如果不存在,请说明理由.

【答案】(1)见解析;(2)y=-2![]() ;(3)点P的坐标为(-5,2),(-4,10).
;(3)点P的坐标为(-5,2),(-4,10).
【解析】
(1)依题意得出MD⊥AB继而推出∠MDA=∠AOB,∠MAD=∠BAO,然后可证明;
(2)设A(0,m),由直线y=2x+12可知,OA=12,OB=6,则AM=12m,DM=2![]() ,利用勾股定理得AB=6
,利用勾股定理得AB=6![]() ,由△ADM∽△AOB,利用相似比求m的值即可,设抛物线顶点式,将M点坐标代入,可求抛物线解析式;
,由△ADM∽△AOB,利用相似比求m的值即可,设抛物线顶点式,将M点坐标代入,可求抛物线解析式;
(3)存在,△AOB中,OA:OB=12:6=2:1,则所求直角三角形两直角边的比为2:1,根据△PAM中,顶点P,A,M分别为直角顶点,根据抛物线解析式分别求符合条件的点P的坐标
(1)∵AB是⊙M的切线,D是切点,
∴MD⊥AB,
∴∠MDA=90°=∠AOB.
又∵∠MAD=∠BAO,
∴△ADM∽△AOB.
(2)设M(0,m),由直线y=-2x+12得OA=12,OB=6,则AM=12-m,而DM=2![]() ,
,
在Rt△AOB中,AB=![]() .,
.,
∵△ADM∽△AOB,
∴![]() ,
,
即![]() ,
,
解得m=2,
∴M(0,2).
设顶点坐标为![]() 的抛物线的函数表达式为y=a
的抛物线的函数表达式为y=a![]() 2+
2+![]() ,将点M的坐标代入,得a
,将点M的坐标代入,得a![]() 2+
2+![]() =2,解得a=-2,
=2,解得a=-2,
∴抛物线的函数表达式为y=-2![]() 2+
2+![]() ;
;
(3)存在.①当顶点M为直角顶点时,M,P两点关于抛物线的对称轴直线x=-![]() 对称,此时MP=5,AM=12-2=10,AMMP=2:,符合题意,此时点P的坐标为(-5,2);
对称,此时MP=5,AM=12-2=10,AMMP=2:,符合题意,此时点P的坐标为(-5,2);
②当顶点A为直角顶点时,点P的纵坐标为12,代入抛物线表达式,得-2![]() 2+
2+![]() =12,解得x=-
=12,解得x=-![]() ,此时AP=
,此时AP=![]() ,AM=10,不符合题意;
,AM=10,不符合题意;
③当顶点P′为直角顶点时,则由相似三角形的性质可设P′的坐标为(n,-2n+2)或(-2m,m+2).若P′(n,-2n+2),则-2n-![]() n=10,解得n=-4;当x=-4时,y=-2×
n=10,解得n=-4;当x=-4时,y=-2×![]() +
+![]() =10,-2n+2=10,符合题意;
=10,-2n+2=10,符合题意;
若P′(-2m,m+2),则4m+m=10,解得m-2,当x=-2m=-4时,y=-2×![]() +
+![]() =10,m+2=4,不符合题意.
=10,m+2=4,不符合题意.
综上所述,符合条件的点P的坐标为(-5,2),(-4,10).