题目内容
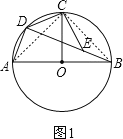
【题目】已知AB是⊙O的直径,半径OC垂直AB,D为弧AC上任意一点,E为弦BD上一点,且BE=AD
(1)试判断△CDE的形状,并加以证明.
(2)若∠ABD=15°,AO=4,求DE的长.

【答案】(1)△CDE为等腰直角三角形,证明详见解析;(2)![]() .
.
【解析】
(1)由条件可证明△ADC≌△BEC,则可得到CD=CE,结合AB为直径可证明∠DCE=90°,可判断△CDE为等腰直角三角形;
(2)由条件可证明△COD为等边三角形,则可求得CD=4,利用勾股定理可求得DE的长.
(1)△CDE为等腰直角三角形,
证明如下:
如图1,连接AC、BC,
则∠DAC=∠DBC,
∵AB为直径,CO⊥AB,
∴△ABC为等腰直角三角形,
∴AC=BC,
在△ADC和△BEC中
![]()
∴△ADC≌△BEC(SAS),
∴CD=CE,∠DCA=∠BCE,
∵∠ACB=90°,
∴∠ACE+∠BCE=90°,
∴∠DCA+∠ACE=90°,即∠DCE=90°,
∴△CDE为等腰直角三角形;
(2)如图2,连接OD,

则∠AOD=2∠ABD=2×15°=30°,
∵∠AOC=90°,
∴∠DOC=60°,且OD=OC=OA=4,
∴△OCD为等边三角形,
∴CD=CE=OA=4,
在Rt△CDE中,由勾股定理可得![]() .
.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目