题目内容
【题目】如图,在四边形ABCD中,AB∥CD,AB=BC,∠B=60°,E是BC边上一点.
(1)如图1,若E是BC的中点,∠AED=60°,求证:CE=CD;
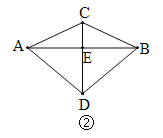
(2)如图2,若∠EAD=60°,求证:△AED是等边三角形.

【答案】(1)见解析;(2)见解析
【解析】
(1)根据AB=BC,∠B=60°得三角形ABC为等边三角形,再根据等边三角形的性质得AE⊥BC,进而证明∠EDC=∠DEC即可;
(2)连接AC,根据两条线平行,同旁内角互补和三角形内角和定理得∠ADC=120°﹣∠BAE,∠AEB=120°﹣∠BAE,即可证明△ABE≌△ACD,进而得结论.
(1)∵AB=BC,∠B=60°,
∴△ABC是等边三角形,
∴∠ACB=60°=∠BAC,
∵E是BC的中点,
∴AE⊥BC,
∴∠AEC=90°,
∵∠AED=60°,
∴∠DEC=30°,
∵AB∥CD,
∴∠ACD=∠BAC=60°,
∴∠ECD=∠ACE+∠ACD=120°,
∴∠CDE=180°﹣120°﹣30°=30°,
∴∠CED=∠CDE,
∴CE=CD.
(2)如图:连接AC,

∵AB=BC,∠B=60°,
∴△ABC是等边三角形,
∴AB=AC,
∵AB∥CD,
∴∠BAD+∠ADC=180°,
∵∠EAD=60°,
∴∠ADC=180°﹣∠EAD﹣∠EAB=120°﹣∠EAB.
在△ABE中,∠AEB=180°﹣∠B﹣∠EAB=120°﹣∠EAB,
∴∠AEB=∠ADC,
∵∠BAE+∠EAC=∠DAC+∠EAC=60°,
∴∠BAE=∠DAC,
∴△ABE≌△ACD(AAS),
∴AE=AD,
∠EAD=60°,
∴△AED是等边三角形.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目