题目内容
【题目】小明在学习过程中遇到这样一个问题：
“一个木箱漂浮在河水中，随河水向下游漂去，在木箱上游和木箱下游各有一条小船，分别为甲船和乙船，两船距木箱距离相等，同时划向木箱，若两船在静水中划行的速度是30m/min，那么哪条小船先遇到木箱？”
小明是这样分析解决的：
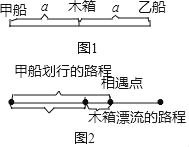
小明想通过比较甲乙两船遇见木箱的时间，知道哪条小船先遇见木箱．设甲船遇见木箱的时间为xmin，乙船遇见木箱的时间为ymin，开始时两船与木箱距离相等，都设为am，如图1．
如图2，利用甲船划行的路程﹣木箱漂流的路程=开始时甲船与木箱的距离：
列方程：x（30+5）﹣5x=a
解得，x=
所以甲船遇见木箱的时间为min．
(1)参照小明的解题思路继续完成上述问题；
(2)借鉴小明解决问题的方法和(1)中发现的结论解决下面问题：
问题：“在一河流中甲乙两条小船，同时从A地出发，甲船逆流而上，乙船顺流而下；划行10分钟后，乙船发现船上木箱不知何时掉入水中，乙船立即通知甲船，两船同时掉头寻找木箱，若两船在静水中划行的速度是v（单位：m/min，v大于5），水流速度是5m/min，两船同时遇见木箱，那么木箱是出发几分钟后掉入水中的？”
【答案】(1)两船同时遇到木箱；(2)木箱是出发0分钟后掉入水中的．
【解析】
(1) 根据乙船划行的路程+木箱漂流的路程=开始时乙船与木箱的距离, 即可列出关于ッ的一元一次方程, 解之即可求出y值, 将x、 y值比较后即可得出结论;
(2) 设木箱是出发份分钟后掉入水中的, 根据(1) 可知10分钟时两船距离木箱的距离相等, 依此即可得出关于t的一元一次方程, 解之即可得出结论.
(1)利用乙船划行的路程+木箱漂流的路程=开始时乙船与木箱的距离：
列方程：y（30﹣5）+5y=a，
解得：y=
∴乙船遇见木箱的时间为min．
∵=
，
∴两船同时遇到木箱．
(2)设木箱是出发t分钟后掉入水中的，
根据题意得：10（v﹣5）+（v+5）t+5（10﹣t）=v（10﹣t），
整理得：2vt=0，
解得：t=0．
答：木箱是出发0分钟后掉入水中的．
