题目内容
【题目】数轴上的点![]() 表示的数是5,点
表示的数是5,点![]() 表示的数是
表示的数是![]() ,这两点都以每秒一个单位长度的速度在数轴上各自朝某个方向运动,且两点同时开始运动:
,这两点都以每秒一个单位长度的速度在数轴上各自朝某个方向运动,且两点同时开始运动:
(1)若点![]() 向右运动,则两秒后点
向右运动,则两秒后点![]() 表示的数是_______;(直接写结果)
表示的数是_______;(直接写结果)
(2)若点![]() 向左运动,点
向左运动,点![]() 向右运动,当这两点相遇时点
向右运动,当这两点相遇时点![]() 表示的数是多少?
表示的数是多少?
(3)同时运动3秒后,这两点相距多远?
【答案】(1)7;(2)相遇时点![]() 表示的数为1;(3)这两点的距离为8或2或14.
表示的数为1;(3)这两点的距离为8或2或14.
【解析】
(1)根据运动速度和时间可得运动距离,结合运动方向可得答案;
(2)首先求出相遇时所用的时间,然后再计算相遇时点![]() 表示的数;
表示的数;
(3)分三种情况讨论:①当同时同向运动3秒后,②当点![]() 向左运动,点
向左运动,点![]() 向右运动时,③当点
向右运动时,③当点![]() 向右运动,点
向右运动,点![]() 向左运动时,分别求解即可.
向左运动时,分别求解即可.
解:(1)∵点![]() 表示的数是5,运动速度为每秒一个单位长度,
表示的数是5,运动速度为每秒一个单位长度,
∴若点![]() 向右运动,则两秒后点
向右运动,则两秒后点![]() 表示的数是5+2×1=7,
表示的数是5+2×1=7,
故答案为:7;
(2)由题意得,A、B之间的距离为:5-(-3)=8,
设相遇时所用时间为t,
则t+t=8,
解得:t=4,
∴相遇时点![]() 表示的数为:5-4×1=1;
表示的数为:5-4×1=1;
(3)分三种情况讨论:
①当同时同向运动3秒后,
∵A,B的速度相同,
∴A、B之间的距离不变,为8;
②当点![]() 向左运动,点
向左运动,点![]() 向右运动时,
向右运动时,
A、B之间的距离为:8-3×1-3×1=2;
③当点![]() 向右运动,点
向右运动,点![]() 向左运动时,
向左运动时,
A、B之间的距离为:8+3×1+3×1=14;
综上,同时运动3秒后,这两点的距离为8或2或14.
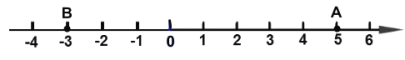

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目