��Ŀ����
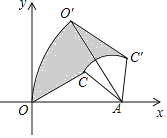
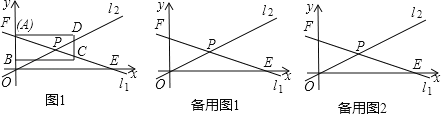
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���F������Ϊ��0��10������E������Ϊ��20��0����ֱ��l1������F�͵�E��ֱ��l1��ֱ��l2 ��y=![]() x�ཻ�ڵ�P��
x�ཻ�ڵ�P��
��1����ֱ��l1�ı���ʽ�͵�P�����ꣻ
��2������ABCD�ı�AB��y����������ϣ���A���F�غϣ���B���߶�OF�ϣ���ADƽ����x �ᣬ��AB=6��AD=9��������ABCD������FE�ķ���ƽ�ƣ���ADʼ����x ��ƽ�У���֪����ABCD��ÿ��![]() ����λ���ٶ������ƶ�����A�ƶ�����Eʱֹ�ƶ��������ƶ�ʱ��Ϊt�루t��0����
����λ���ٶ������ƶ�����A�ƶ�����Eʱֹ�ƶ��������ƶ�ʱ��Ϊt�루t��0����
�پ���ABCD���ƶ������У�B��C��D����������ֻ��һ����������ֱ��l1��l2�ϣ���ֱ��д����ʱt��ֵ��
��������ABCD���ƶ��Ĺ����У�ֱ��CD��ֱ��l1�ڵ�N����ֱ��l2�ڵ�M������PMN���������18ʱ����ֱ��д����ʱt��ֵ��
���𰸡���1��ֱ��l1�ı���ʽΪy=��![]() x+10����P����Ϊ��8��6������2����tֵΪ
x+10����P����Ϊ��8��6������2����tֵΪ![]() ��
��![]() ���ڵ�t=
���ڵ�t=![]() ʱ����PMN���������18.
ʱ����PMN���������18.
����������1�����ô���ϵ���������ʽ��������ϵʽ���������㣻
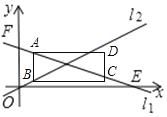
��2���ٷ��������˶����ɣ��ҵ���D�͵�B�ֱ���ֱ��l2�ϻ���ֱ��l1��ʱ�����������AD��AB�ֱ���Կ���ͼ������ꡢ������֮��췽�����A���꣬�������AF���룻
�����A���꣬��ʾ��PMN���ɣ�
��1����ֱ��l1�ı���ʽΪy=kx+b��
��ֱ��l1����F��0��10����E��20��0����
��![]() �������
�������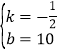 ��
��
ֱ��l1�ı���ʽΪy=��![]() x+10��
x+10��
�ⷽ���� ��
��![]() ��
��
���P������8��6����
��2������ͼ������D��ֱ����l2ʱ��

��AD=9
���D���A�ĺ�����֮��Ϊ9��
�ཫֱ��l1��ֱ��l2 �Ľ���ʽ����Ϊx=20��2y��x=![]() y��
y��
��![]() y����20��2y��=9��
y����20��2y��=9��
�����y=![]() ��
��
��x=20��2y=![]() ��
��
���A����������![]() ��
��![]() ����
����
��AF=![]() ��
��
�ߵ�A�ٶ�Ϊÿ��![]() ����λ��
�����
��t=![]() ��
��
��ͼ������B��l2 ֱ����ʱ��
��AB=6��
���A��������ȵ�B���������6����λ��
��ֱ��l1�Ľ���ʽ��ȥֱ��l2 �Ľ���ʽ����
��![]() x+10��
x+10��![]() x=6��
x=6��
���x=![]() ��
��
y=��![]() x+10=
x+10=![]() ��
��
���A������![]() ��
��![]() ��
��
��AF=![]() ��
��
�ߵ�A�ٶ�Ϊÿ��![]() ����λ��
�����
��t=![]() ��
��
��tֵΪ![]() ��
��![]() ��
��
����ͼ��
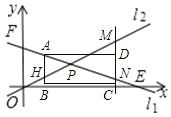
��ֱ��AB��l2 �ڵ�H��
���A������Ϊa�����D������Ϊa+9��
�ɢ��з�����֪��MN=![]() ��
��
��ʱ��P��MN����Ϊ��a+9��8=a+1��
�ߡ�PMN���������18��
��![]() =18��
=18��
���
a1=![]() -1��a2=��
-1��a2=��![]() -1����ȥ����
-1����ȥ����
��AF=6��![]() ��
��
���ʱtΪ![]() ��
��
��t=![]() ʱ����PMN���������18.
ʱ����PMN���������18.