Question

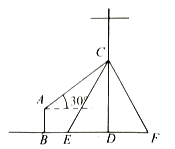
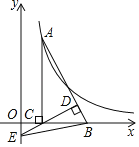
【题目】如图，点A在反比例函数y＝（x＞0）的图象上，AC⊥x轴，垂足为C，B在OC延长线上，∠CAB＝30°，直线CD⊥AB，CD与AB和y轴交点分别为D，E，连接BE，△BCE的面积为1，则k的值是_______．

Answer 1

【答案】6

【解析】

根据题意设A（n，m），B（t，0），则OC=n，AC=m，解直角三角形求出BC和OE的长，然后利用三角形的面积公式可得到mn=6，即得到k的值．

解：设A（n，m），则OC＝n，AC＝m，

∵AC⊥BC，∠CAB＝30°，

∴∠ABC＝60°，

∵CD⊥AB，

∴∠OCE＝∠BCD＝30°，

在Rt△ABC中，BC＝AC＝m，

在Rt△EOC中，OE＝OC＝n，

∵△BCE的面积为1，

∴S△BCE＝OEBC＝1，

∴nm＝1，

∴mn＝6，

∵点A在反比例函数y＝（x＞0）的图象上，

∴k＝mn＝6．

故答案为6．