题目内容
如图(1),矩形ABCD的一边BC在直角坐标系中x轴上,折叠边AD,使点D落在x轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为(m,0),其中m>0.
(1)求点E、F的坐标(用含m的式子表示);
(2)连接OA,若△OAF是等腰三角形,求m的值;
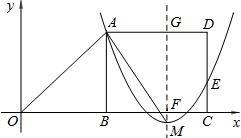
(3)如图(2),设抛物线y=a(x-m-6)2+h经过A、E两点,其顶点为M,连接AM,若∠OAM=90°,求a、h、m的值.

(1)求点E、F的坐标(用含m的式子表示);
(2)连接OA,若△OAF是等腰三角形,求m的值;
(3)如图(2),设抛物线y=a(x-m-6)2+h经过A、E两点,其顶点为M,连接AM,若∠OAM=90°,求a、h、m的值.

(1)∵四边形ABCD是矩形,
∴AD=CB=10,AB=DC=8,∠D=∠DCB=∠ABC=90°,
由折叠对称性:AF=AD=10,EF=DE,
在Rt△ABF中,BF=
=
=6,
∴CF=4,
设EF=x,则EC=8-x,
在Rt△ECF中,42+(8-x)2=x2,
解得:x=5,
∴CE=3,
∵B(m,0),
∴E(m+10,3),F(m+6,0);
(2)分三种情况讨论:
若AO=AF,
∵AB⊥OF,
∴BO=BF=6,
∴m=6,
若OF=FA,则m+6=10,
解得:m=4,
若AO=OF,在Rt△AOB中,AO2=OB2+AB2=m2+64,
∴(m+6)2=m2+64,
解得:m=
,
∴m=6或4或
;
(3)由(1)知:E(m+10,3),A(m,8).
∴
,
得
,
∴M(m+6,-1),
设对称轴交AD于G,
∴G(m+6,8),
∴AG=6,GM=8-(-1)=9,
∵∠OAB+∠BAM=90°,∠BAM+∠MAG=90°,
∴∠OAB=∠MAG,
∵∠ABO=∠MGA=90°,
∴△AOB∽△AMG,
∴
=
,
即:
=
,
∴m=12,
∴AD=CB=10,AB=DC=8,∠D=∠DCB=∠ABC=90°,
由折叠对称性:AF=AD=10,EF=DE,
在Rt△ABF中,BF=
| AF2-AB2 |
| 100-64 |
∴CF=4,
设EF=x,则EC=8-x,
在Rt△ECF中,42+(8-x)2=x2,
解得:x=5,
∴CE=3,
∵B(m,0),
∴E(m+10,3),F(m+6,0);
(2)分三种情况讨论:
若AO=AF,
∵AB⊥OF,
∴BO=BF=6,
∴m=6,
若OF=FA,则m+6=10,
解得:m=4,
若AO=OF,在Rt△AOB中,AO2=OB2+AB2=m2+64,
∴(m+6)2=m2+64,
解得:m=
| 7 |
| 3 |
∴m=6或4或
| 7 |
| 3 |
(3)由(1)知:E(m+10,3),A(m,8).
∴
|
得
|
∴M(m+6,-1),
设对称轴交AD于G,
∴G(m+6,8),
∴AG=6,GM=8-(-1)=9,
∵∠OAB+∠BAM=90°,∠BAM+∠MAG=90°,
∴∠OAB=∠MAG,
∵∠ABO=∠MGA=90°,
∴△AOB∽△AMG,
∴
| OB |
| MG |
| AB |
| AG |
即:
| m |
| 9 |
| 8 |
| 6 |
∴m=12,


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 落在点D的位置.
落在点D的位置.

