Question

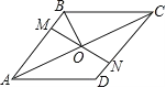
【题目】在矩形ABCD中，将点A翻折到对角线BD上的点M处，折痕BE交AD于点E．将点C翻折到对角线BD上的点N处，折痕DF交BC于点F．

（1）求证：四边形BFDE为平行四边形；

（2）若四边形BFDE为菱形，且AB＝2，求BC的长．

Answer 1

【答案】（1）证△ABE≌△CDF，推出AE=CF，求出DE=BF，DE∥BF，根据平行四边形判定推出即可．

（2）

【解析】

（1）证△ABE≌△CDF，推出AE=CF，求出DE=BF，DE∥BF，根据平行四边形判定推出即可．

（2）求出∠ABE=30°，根据直角三角形性质求出AE、BE，即可求出答案．

解：（1）证明：∵四边形ABCD是矩形，∴∠A=∠C=90°，AB=CD，AB∥CD．∴∠ABD=∠CDB．

∵在矩形ABCD中，将点A翻折到对角线BD上的点M处，折痕BE交AD于点E．将点C翻折到对角线BD上的点N处，

∴∠ABE=∠EBD=∠ABD，∠CDF=∠CDB．∴∠ABE=∠CDF．

在△ABE和△CDF中，∵，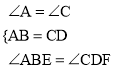

∴△ABE≌△CDF（ASA）．∴AE=CF．

∵四边形ABCD是矩形，∴AD=BC，AD∥BC．

∴DE=BF，DE∥BF．∴四边形BFDE为平行四边形．

（2）∵四边形BFDE为为菱形，∴BE=ED，∠EBD=∠FBD=∠ABE．

∵四边形ABCD是矩形，∴AD=BC，∠ABC=90°．∴∠ABE=30°．

∵∠A=90°，AB=2，∴，．

∴BC=AD=AE+ED=AE+BE=．