Question

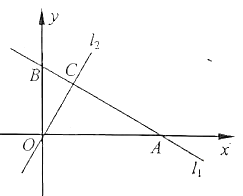
【题目】如图，在平面直角坐标系中，一次函数的图象分别与轴、轴交于两点，正比例函数的图象与交于点.

（1）求点坐标；

（2）求的表达式；

（3）求和的面积.

Answer 1

【答案】（1）C(2,4);(2) ;(3) ;

【解析】

（1）根据C点在上，将C点坐标代入解析式，可得m的值，进而求出C点坐标；

（2）由（1）得C点坐标，由待定系数法可以求出的解析式.

（3）过点C作CD⊥AO于D，CE⊥BO于E，则CD=4,CE=2,再根据A（10，0），B （0，5）可得AO=10,OB=5,进而求出和的面积.

（1）把点C(m,4)代入一次函数中，得：

解得：

∴C（2，4）

（2）设的解析式为，将C(2,4)代入得：

∴的解析式为：.

（3）如图，过点C作CD⊥AO于D，CE⊥BO于E，则CD=4,CE=2,

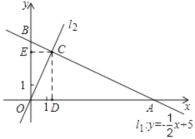
由得：

时，，即B （0，5）；

时，，即A（10，0），

∴AO=10,OB=5,

∴;