题目内容
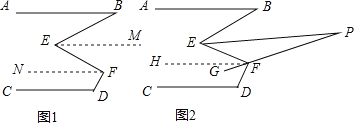
【题目】如图1,已知AB∥CD,∠B=20°,∠D=110°.
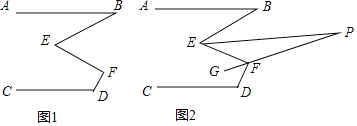
(1)若∠E=50°,请直接写出∠F的度数;
(2)探索∠E与∠F之间满足的数量关系,并说明理由;
(3)如图2,EP平分∠BEF,FG平分∠EFD,FG的反向延长线交EP于点P,求∠P的度数.
【答案】(1)100°;(2)∠F=∠E+50°,理由见解析;(3)∠P=25°
【解析】
(1)如图1,分别过点E,F作EM∥AB,FN∥AB,根据平行线的性质得到∠B=∠BEM=20°,∠MEF=∠EFN,∠D+∠DFN=180°,代入数据即可得到结论;
(2)如图1,根据平行线的性质得到∠B=∠BEM=20°,∠MEF=∠EFN,由AB∥CD,AB∥FN,得到CD∥FN,根据平行线的性质得到∠D+∠DFN=180°,于是得到结论;
(3)如图2,过点F作FH∥EP,设∠BEF=2x°,则∠EFD=(2x+50)°,根据角平分线的定义得到∠PEF=![]() ∠BEF=x°,∠EFG=
∠BEF=x°,∠EFG=![]() ∠EFD=(x+25)°,根据平行线的性质得到∠PEF=∠EFH=x°,∠P=∠HFG,于是得到结论.
∠EFD=(x+25)°,根据平行线的性质得到∠PEF=∠EFH=x°,∠P=∠HFG,于是得到结论.
解:(1)如图1,分别过点E,F作EM∥AB,FN∥AB,
∴EM∥AB∥FN,
∴∠B=∠BEM=20°,∠MEF=∠EFN,
又∵AB∥CD,AB∥FN,
∴CD∥FN,
∴∠D+∠DFN=180°,
又∵∠D=110°,
∴∠DFN=70°,
∴∠BEF=∠MEF+20°,∠EFD=∠EFN+70°,
∴∠EFD=∠MEF+70°
∴∠EFD=∠BEF+50°=100°;
故答案为:100°;
(2)如图1,分别过点E,F作EM∥AB,FN∥AB,
∴EM∥AB∥FN,
∴∠B=∠BEM=20°,∠MEF=∠EFN,
又∵AB∥CD,AB∥FN,
∴CD∥FN,
∴∠D+∠DFN=180°,
又∵∠D=110°,
∴∠DFN=70°,
∴∠BEF=∠MEF+20°,∠EFD=∠EFN+70°,
∴∠EFD=∠MEF+70°,
∴∠EFD=∠BEF+50°;
(3)如图2,过点F作FH∥EP,
由(2)知,∠EFD=∠BEF+50°,
设∠BEF=2x°,则∠EFD=(2x+50)°,
∵EP平分∠BEF,GF平分∠EFD,
∴∠PEF=![]() ∠BEF=x°,∠EFG=
∠BEF=x°,∠EFG=![]() ∠EFD=(x+25)°,
∠EFD=(x+25)°,
∵FH∥EP,
∴∠PEF=∠EFH=x°,∠P=∠HFG,
∵∠HFG=∠EFG﹣∠EFH=25°,
∴∠P=25°.

 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案【题目】嘉淇同学为了探索泥茶壶盛水喝起来凉的原因,对泥茶壶和塑料壶盛水散热情况进行对比实验.在同等情况下,把稍高于室温(25.5℃)的水放入凉壶中,每隔一小时同时测出凉壶水温,所得数据如下表:
刚倒入时 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
泥茶壶 | 34 | 27 | 25 | 23.5 | 23.0 | 22.5 | 22.5 | 22.5 |
塑料壶 | 34 | 30 | 27 | 26.0 | 25.5 | 22.5 | 22.5 | 22.5 |
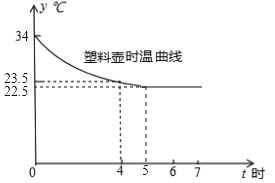
(1)塑料壶水温变化曲线如图,请在同一坐标系中,画出泥壶水温的变化曲线;
(2)比较泥壶和塑料壶水温变化情况的不同点.