题目内容
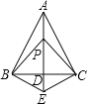
【题目】如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD,OP是∠BOC的平分线,

⑴写出所有∠EOC的补角 ;
⑵如果∠AOD=40°,求∠POF的度数.
【答案】(1)∠EOD,∠AOF都是∠EOC的补角;(2)∠POD=70°.
【解析】
(1)首先根据垂直定义可得∠AOE=∠DOF=90°,然后再证明∠EOD=∠AOF,根据补角定义可得∠EOD,∠AOF都是∠EOC的补角;
(2)根据对顶角相等,可得∠BOC的度数,根据角平分线的定义,可得∠COP,根据余角的定义,可得答案.
(1)∵OE⊥AB,OF⊥CD,
∴∠AOE=∠DOF=90°,
∴∠EOA+∠AOD=∠DOF+∠AOD,
即:∠EOD=∠AOF,
∵∠EOC+∠EOD=180°,
∴∠AOF+∠EOC=180°,
∴∠EOD,∠AOF都是∠EOC的补角;
(2)由对顶角相等,得∠BOC=∠AOD=40°,
由OP是∠BOC的平分线,得∠COP=![]() ∠BOC=20°,
∠BOC=20°,
由余角的定义,得∠POD=∠COD-∠COP=90°-20°=70°.

练习册系列答案
相关题目