题目内容
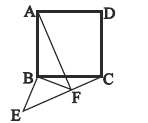
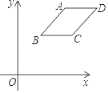
【题目】如图,已知菱形ABCD,四个顶点坐标分别为A(m,n),B(1,2),C(m+![]() ﹣1,2),D(m+
﹣1,2),D(m+![]() ,n).求m,n的值.
,n).求m,n的值.
【答案】m=2,n=3.
【解析】
由菱形的性质得到AB=BC=CD=AD,AD∥BC,根据已知条件求得m的大小;过A作AM⊥BC于点M,由勾股定理得到AM的大小,从而得到m.
∵四边形ABCD为菱形,
∴AB=BC=CD=AD,AD∥BC,
∵A(m,n),B(1,2),C(m+![]() ﹣1,2),D(m+
﹣1,2),D(m+![]() ,n),
,n),
∴AD=m+![]() ﹣m=
﹣m=![]() ,
,
BC=m+![]() ﹣1﹣1=m+
﹣1﹣1=m+![]() ﹣2,
﹣2,
∴![]() =m+
=m+![]() ﹣2,
﹣2,
∴m=2,
∴A(2,n),
如图,过点A作AM⊥BC于点M,
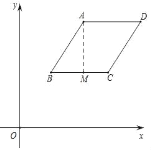
在Rt△ABM中,BM=xA﹣xB=2﹣1=1,AB=![]() ,
,
∴AM=![]() =1,
=1,
∴n=yA=yB+1=2+1=3,
∴m=2,n=3.

练习册系列答案
相关题目
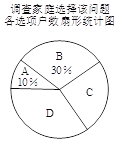
【题目】某班同学为了解2019年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行整理如下:
月均用水量x(t) | 频数(户) | 频率 |
| 6 | 0.12 |
| 0.24 | |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | |
| 2 | 0.04 |

请解答下列问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)求该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?