题目内容
【题目】在平面直角坐标系中,四边形![]() 是矩形,点
是矩形,点![]() ,点
,点![]() ,点
,点![]() .以
.以![]() 点为中心,顺时针旋转矩形
点为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 的对应点分别为
的对应点分别为![]() ,记旋转角为
,记旋转角为![]() .
.
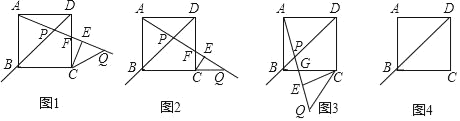
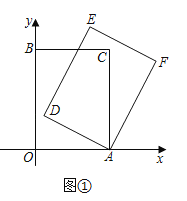
(1)如图①,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
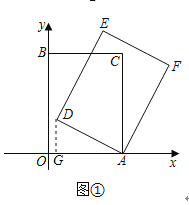
(2)如图②,当点![]() 落在
落在![]() 的延长线上时,求点
的延长线上时,求点![]() 的坐标;
的坐标;

(3)当点![]() 落在线段
落在线段![]() 上时,求点
上时,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
【答案】(1)点![]() 的坐标为
的坐标为![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() .
.
【解析】
(1) 过点![]() 作
作![]() 轴于
轴于![]() 根据已知条件可得出AD=6,再直角三角形ADG中可求出DG,AG的长,即可确定点D的坐标.
根据已知条件可得出AD=6,再直角三角形ADG中可求出DG,AG的长,即可确定点D的坐标.
(2) 过点![]() 作
作![]() 轴于
轴于![]() 于
于![]() 可得出
可得出![]() ,根据勾股定理得出AE的长为10,再利用面积公式求出DH,从而求出OG,DG的长,得出答案
,根据勾股定理得出AE的长为10,再利用面积公式求出DH,从而求出OG,DG的长,得出答案
(3) 连接![]() ,作
,作![]() 轴于G,由旋转性质得到
轴于G,由旋转性质得到![]() ,从而可证
,从而可证![]() ,继而可得出结论.
,继而可得出结论.
解:(1)过点![]() 作
作![]() 轴于
轴于![]() ,如图①所示:
,如图①所示:
![]() 点
点![]() ,点
,点![]() .
.
![]() ,
,
![]() 以点
以点![]() 为中心,顺时针旋转矩形
为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ;
;
(2)过点![]() 作
作![]() 轴于
轴于![]() 于
于![]() ,如图②所示:
,如图②所示:

则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,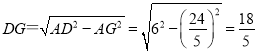 ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ;
;
(3)连接![]() ,作
,作![]() 轴于G,如图③所示:
轴于G,如图③所示:
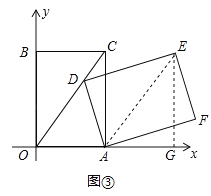
由旋转的性质得:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,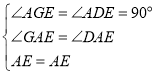 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目