题目内容
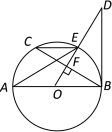
【题目】如图,AB是⊙O直径,OD⊥弦BC与点F,且交⊙O于点E,且∠AEC=∠ODB.
(1)判断直线BD和⊙O的位置关系,并给出证明;
(2)当tan∠AEC=![]() ,BC=8时,求OD的长.
,BC=8时,求OD的长.
【答案】(1)直线BD和⊙O相切,证明见解析;(2)![]()
【解析】(1)因为同弧所对的圆周角相等,所以有∠AEC=∠ABC,又∠AEC=∠ODB,所以∠ABC=∠ODB,OD⊥弦BC,即∠ABC+∠BOD=90°,则有∠ODB+∠BOD=90°,即BD垂直于AB,所以BD为切线.
(2)由垂径定理可得FB=FC=4,再由三角关系得到DF=![]() ,BD可由勾股定理求出,再由△DBF∽△ODB,并根据对应线段成比例求出OD.
,BD可由勾股定理求出,再由△DBF∽△ODB,并根据对应线段成比例求出OD.
解:(1)直线BD和⊙O相切
证明:∵∠AEC=∠ODB,∠AEC=∠ABC
∴∠ABC=∠ODB
∵OD⊥BC
∴∠DBC+∠ODB=90°
∴∠DBC+∠ABC=90°
∴∠DBO=90°
∴直线BD和⊙O相切.
(2)∵OD⊥BC
∴FB=FC=4
∵tan∠AEC=tan∠ODB=3:4
∴BF:DF =3:4 ,
∴DF=![]()
利用勾股定理可求得BD=![]()
通过证明△DBF∽△ODB,利用相似比可得OD:DB=BD:FD
所以求出OD=![]()

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目