题目内容
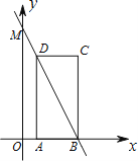
【题目】如图,在平面直角坐标系xOy中,矩形ABCD的边AD=3,A(![]() ,0),B(2,0),直线y=kx+b(k≠0)经过B,D两点.
,0),B(2,0),直线y=kx+b(k≠0)经过B,D两点.
(1)求直线y=kx+b(k≠0)的表达式;
(2)若直线y=kx+b(k≠0)与y轴交于点M,求△CBM的面积.
【答案】(1)y=-2x+4;(2)S△BCM=3.
【解析】
(1)利用矩形的性质,得出点D坐标,再利用待定系数法求得函数解析式;
(2)由三角形的面积公式,即可解答.
(1)∵在矩形ABCD中,AD=3,A(![]() ,0),B(2,0),
,0),B(2,0),
∴D(![]() ,3),C(2,3).
,3),C(2,3).
把B(2,0),D(![]() ,3)代入y=kx+b(k≠0)得:
,3)代入y=kx+b(k≠0)得: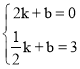 ,解得:
,解得:![]() ,
,
∴直线表达式为:y=-2x+4;
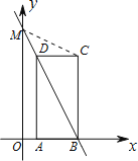
(2)连接CM.
∵B(2,0),
∴OB=2.
∴S△BCM=![]() BCOB=
BCOB=![]() ×3×2=3.
×3×2=3.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
【题目】某中学开展“数学史”知识竞赛活动,八年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示:
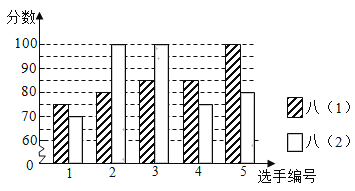
(1)根据图示填写下表a、b、c的值:
统计量 班别 | 平均数(分) | 中位数(分) | 众数(分) |
八年(1)班 | a | 85 | c |
八年(2)班 | 85 | b | 100 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班的选于复赛成绩较好;
(3)通过计算八年(1)班5名选手的复赛成绩的方差S八(1)2=70,请你计算八年(2)班5名选手复赛成绩的方差并判断哪个班的选手复赛成绩较为均衡.