题目内容
【题目】经过三边都不相等的三角形的一个顶点的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
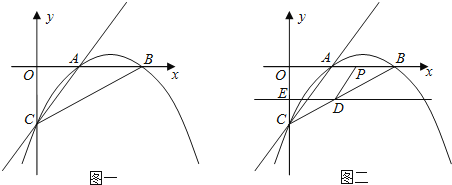
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线
(2)在△ABC中,∠A=52°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=3,BC=2,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
【答案】(1)详见解析;(2)∠ACB=96°或104°;(3)![]() .
.
【解析】试题分析:(1)根据完美分割线的定义只要证明①△ABC不是等腰三角形,②△ACD是等腰三角形,③△BDC∽△BCA即可.
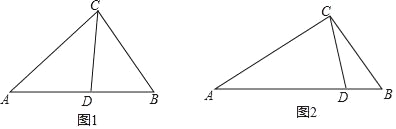
(2)分三种情形讨论即可①如图2,当AD=CD时,②如图3中,当AD=AC时,③如图4中,当AC=CD时,分别求出∠ACB即可.
(3)设BD=x,利用△BCD∽△BAC,得![]() ,列出方程即可求出BD的长,然后再根据相似三角形的性质即可求出CD的长.
,列出方程即可求出BD的长,然后再根据相似三角形的性质即可求出CD的长.
试题解析:
(1)证明:如图1中,
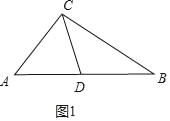
∵∠A=40°,∠B=60°,
∴∠ACB=80°,
∴△ABC不是等腰三角形,
∵CD平分∠ACB,
∴∠ACD=∠BCD=![]() ∠ACB=40°,
∠ACB=40°,
∴∠ACD=∠A=40°,
∴△ACD为等腰三角形,
∵∠DCB=∠A=40°,∠CBD=∠ABC,
∴△BCD∽△BAC,
∴CD是△ABC的完美分割线.
(2)①当AD=CD时,如图2,

∠ACD=∠A=52°,
∵△BDC∽△BCA,
∴∠BCD=∠A=52°,
∴∠ACB=∠ACD+∠BCD=104°.
②当AD=AC时,如图3中,
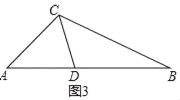
∠ACD=∠ADC=![]() =64°,
=64°,
∵△BDC∽△BCA,
∴∠BCD=∠A=52°,
∴∠ACB=∠ACD+∠BCD=116°.
③当AC=CD时,如图4中,

∠ADC=∠A=52°,
∵△BDC∽△BCA,
∴∠BCD=∠A=52°,
∴∠ADC=∠BCD
∵∠ADC>∠BCD,矛盾,舍弃.
综上所述,∠ACB=96°或104°.
(3)由已知AC=AD=3,
∵△BCD∽△BAC,
∴![]() =
=![]() ,设BD=x,
,设BD=x,
∴22=x(x+3),
∵x>0,
∴x=1,
∵△BCD∽△BAC,
∴![]() =
=![]() ,即
,即![]() ,
,
∴CD=![]() .
.