��Ŀ����
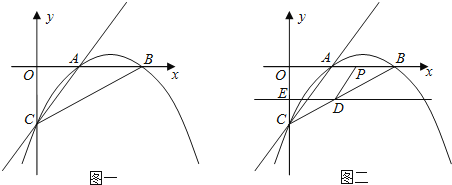
����Ŀ����֪����ͼһ��������![]() ��x�������ύ��A��B���㣬��y�ύ�ڵ�C��ֱ��
��x�������ύ��A��B���㣬��y�ύ�ڵ�C��ֱ��![]() ����A��C���㣬��
����A��C���㣬��![]() ��
��
![]() �������ߵĽ���ʽ��
�������ߵĽ���ʽ��
![]() ��ֱ��DEƽ����x�Ტ��C�㿪ʼ��ÿ��1����λ���ٶ���y��������ƽ�ƣ��ҷֱ�y�ᡢ�߶�BC�ڵ�E��D��ͬʱ����P�ӵ�B��������BO������ÿ��2����λ�ٶ��˶���
��ֱ��DEƽ����x�Ტ��C�㿪ʼ��ÿ��1����λ���ٶ���y��������ƽ�ƣ��ҷֱ�y�ᡢ�߶�BC�ڵ�E��D��ͬʱ����P�ӵ�B��������BO������ÿ��2����λ�ٶ��˶���![]() ��ͼ
��ͼ![]() ������P�˶���ԭ��Oʱ��ֱ��DE���P��ֹͣ�˶�����DP������P�˶�ʱ��Ϊt�룻��
������P�˶���ԭ��Oʱ��ֱ��DE���P��ֹͣ�˶�����DP������P�˶�ʱ��Ϊt�룻��![]() ����tΪ��ֵʱ��s����Сֵ���������Сֵ��
����tΪ��ֵʱ��s����Сֵ���������Сֵ��
![]() ��
��![]() �������£��Ƿ����t��ֵ��ʹ��P��B��DΪ�������������
�������£��Ƿ����t��ֵ��ʹ��P��B��DΪ�������������![]() ���ƣ������ڣ���t��ֵ���������ڣ���˵�����ɣ�
���ƣ������ڣ���t��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��y=![]() ��(2)
��(2)![]() ʱ��s����Сֵ������СֵΪ1��(3)
ʱ��s����Сֵ������СֵΪ1��(3)![]() ��
��![]() .
.
��������������
��1���������õ�A��B��C������ֱ�Ϊ��2��0������4��0���ͣ�0��-2�������ô���ϵ������������ߵĽ���ʽ���ɣ�
��2���ɣ�1�������õ�A��B��C������ɵ�OB=4��OC=2���ɴ˿ɵ�tan��OCB=2�����CE=t���ɵ�DE=2t�����OP=OB-PB=4-2t�����ú�t�Ĵ���ʽ�����S����϶��κ��������ʼ������tΪ��ֵʱ��S��С����Сֵ�Ƕ����ˣ�
��3����OB=5��OC=2��BC=![]() ����EC=t��DE=2t��CD=
����EC=t��DE=2t��CD=![]() ���Ӷ��ɵ�BD=
���Ӷ��ɵ�BD=![]() ������ABC=��PBD��֪��t��ֵ����
������ABC=��PBD��֪��t��ֵ����![]() ��
��![]() ʱ�������������ƽ��м������ۼ�����ö�Ӧ��t��ֵ.
ʱ�������������ƽ��м������ۼ�����ö�Ӧ��t��ֵ.
��⣺
![]() ��ֱ�ߣ�
��ֱ�ߣ�![]() ֪��
֪��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ����
����![]() ��
��
�������ߵĽ���ʽΪ��![]() ������
������![]() ���ã�
���ã�
![]() �����
�����![]()
�������ߵĽ���ʽ��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
�൱![]() ʱ��s����Сֵ������СֵΪ1��
ʱ��s����Сֵ������СֵΪ1��
![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��
��![]() ��
��
��P��B��DΪ�������������![]() ���ƣ���֪
���ƣ���֪![]() ���������������
���������������
![]() �����
�����![]() ��
��
![]() �����
�����![]() ��
��
���ϣ���![]() ��
��![]() ʱ����P��B��DΪ�������������
ʱ����P��B��DΪ�������������![]() ���ƣ�
���ƣ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�