题目内容
【题目】某班要在一面墙上同时展示数张形状、大小均相同的矩形绘画作品，将这些作品排成一个矩形（作品不完全重合）．现需要在每张作品的四个角落都钉上图钉，如果作品有角落相邻，那么相邻的角落共享一枚图钉（例如用9枚图钉将4张作品钉在墙上如图）．若有28枚图钉可供选用，则最多可以展示绘画作品（ ）
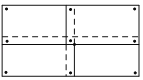
A. 16张B. 18张C. 20张D. 21张
【答案】B
【解析】
分别找出展示的绘画作品展示成一行、二行、三行、四行、五行的时候，28枚图钉最多可以展示的画的数量，比较后即可得出结论．
解：①如果所有的画展示成一行，28÷（1+1）﹣1＝13（张），
∴28枚图钉最多可以展示13张画；
②如果所有的画展示成两行，28÷（2+1）＝9……1（枚），
9﹣1＝8（张），2×8＝16（张），
∴28枚图钉最多可以展示16张画；
③如果所有的画展示成三行，28÷（3+1）＝7，
7﹣1＝6，3×6＝18（张），
∴28枚图钉最多可以展示18张画；
④如果所有的画展示成四行，28÷（4+1）＝5……3（枚），
5﹣1＝4（张），4×4＝16（张），
∴28枚图钉最多可以展示16张画；
⑤如果所有的画展示成五行，28÷（5+1）＝4，
4﹣1＝3（张），5×3＝15（张），
∴28枚图钉最多可以展示15张画．
综上所述：28枚图钉最多可以展示18张画．
故选：B．
期末冲刺100分创新金卷完全试卷系列答案
【题目】某淘宝商家计划平均每天销售某品牌儿童滑板车100辆，但由于种种原因，实际每天的销售量与计划量相比有出入。下表是某周的销售情况（超额记为正、不足记为负）：
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 | +4 | -3 | -5 | +14 | -8 | +21 | -6 |
（1）根据记录的数据可知该店前三天共销售该品牌儿童滑板车______辆。
（2）根据记录的数据可知销售量最多的一天比销售量最少的一天多销售______辆。
（3）该店实行每日计件工资制，每销售一辆车可得40元，若超额完成任务，则超过部分每辆另奖15元；少销售一辆扣20元，那么该店铺的销售人员这一周的工资总额是多少元？
