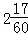题目内容
已知正比例函数y=kx与反比例函数y= 相交于点A(1,b)、点B(c,﹣2),求k+a的值.甲同学说:未知数太多,很难求的;乙同学说:可能不是用待定系数法来求;丙说:如果用数形结合的方法,利用两交点在坐标系中位置的特殊性,可以试试.请结合他们的讨论求出k+a= .
相交于点A(1,b)、点B(c,﹣2),求k+a的值.甲同学说:未知数太多,很难求的;乙同学说:可能不是用待定系数法来求;丙说:如果用数形结合的方法,利用两交点在坐标系中位置的特殊性,可以试试.请结合他们的讨论求出k+a= .
 相交于点A(1,b)、点B(c,﹣2),求k+a的值.甲同学说:未知数太多,很难求的;乙同学说:可能不是用待定系数法来求;丙说:如果用数形结合的方法,利用两交点在坐标系中位置的特殊性,可以试试.请结合他们的讨论求出k+a= .
相交于点A(1,b)、点B(c,﹣2),求k+a的值.甲同学说:未知数太多,很难求的;乙同学说:可能不是用待定系数法来求;丙说:如果用数形结合的方法,利用两交点在坐标系中位置的特殊性,可以试试.请结合他们的讨论求出k+a= .﹣4或4
把A(1,b)代入得出b=k,a=b,求出k=a=b,把B(c,﹣2)代入得:﹣2=ck,﹣2=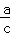 ,求出ck=﹣2,a=﹣2c,推出﹣2c=
,求出ck=﹣2,a=﹣2c,推出﹣2c=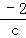 ,求出c的值,即可求出k和a的值,再代入求出即可.
,求出c的值,即可求出k和a的值,再代入求出即可.
解:把A(1,b)代入得:b=k,a=b×1=b,
∴k=a=b,
把B(c,﹣2)代入得:﹣2=ck,﹣2=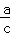 ,
,
∴ck=﹣2,a=﹣2c,
∴k=﹣2c=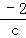 ,
,
解得:c=±1,
当c=1时,k=a=b=﹣2c=﹣2,
k+a=﹣2+(﹣2)=﹣4;
当c=﹣1时,k=a=b=﹣2c=2,
k+a=2+2=4.
故答案为:﹣4或4.
试题分析:
点评:本题考查了一次函数和反比例函数的交点问题和图象上点的坐标特征等知识点,主要考查学生的化简能力和理解能力,题目比较好,有一定的难度.
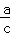 ,求出ck=﹣2,a=﹣2c,推出﹣2c=
,求出ck=﹣2,a=﹣2c,推出﹣2c=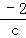 ,求出c的值,即可求出k和a的值,再代入求出即可.
,求出c的值,即可求出k和a的值,再代入求出即可.解:把A(1,b)代入得:b=k,a=b×1=b,
∴k=a=b,
把B(c,﹣2)代入得:﹣2=ck,﹣2=
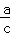 ,
,∴ck=﹣2,a=﹣2c,
∴k=﹣2c=
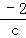 ,
,解得:c=±1,
当c=1时,k=a=b=﹣2c=﹣2,
k+a=﹣2+(﹣2)=﹣4;
当c=﹣1时,k=a=b=﹣2c=2,
k+a=2+2=4.
故答案为:﹣4或4.
试题分析:
点评:本题考查了一次函数和反比例函数的交点问题和图象上点的坐标特征等知识点,主要考查学生的化简能力和理解能力,题目比较好,有一定的难度.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
 ,点M
,点M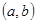 在反比例函数
在反比例函数 的图象上,则反比例函数的解析式为( )
的图象上,则反比例函数的解析式为( )


 的图象相交于点A(﹣1,2)、点B(﹣4,n)
的图象相交于点A(﹣1,2)、点B(﹣4,n)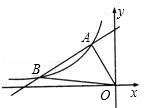
 (x>0)交于A、B两点,与x轴、y轴分别交于E、F两点,连接OA、OB,若S△AOB=S△OBF+S△OAE,则b= .
(x>0)交于A、B两点,与x轴、y轴分别交于E、F两点,连接OA、OB,若S△AOB=S△OBF+S△OAE,则b= .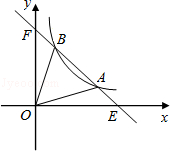
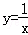 的图象,当x取1,2,3,…,n时,对应在反比例图象上的点分别为M1,M2,M3…,Mn,则
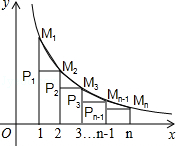
的图象,当x取1,2,3,…,n时,对应在反比例图象上的点分别为M1,M2,M3…,Mn,则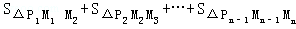 = .
= .
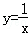 的交点是A(a,4),B(﹣1,b),则这条直线的关系式为( )
的交点是A(a,4),B(﹣1,b),则这条直线的关系式为( )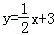
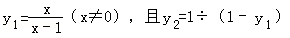 ,y3=1÷(1﹣y2),y4=1÷(1﹣y3),…,yn=1÷(1﹣yn﹣1).则写出y与x的关系式:y4= ,由此可得y2011= .
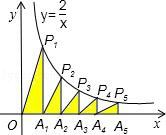
,y3=1÷(1﹣y2),y4=1÷(1﹣y3),…,yn=1÷(1﹣yn﹣1).则写出y与x的关系式:y4= ,由此可得y2011= . 的图象交于点P1、P2、P3、P4、P5…,并设△OA1P1、△A1A2P2、△A2A3P3…面积分别为S1、S2、S3…,按此作法进行下去,则Sn的值为 (n为正整数).
的图象交于点P1、P2、P3、P4、P5…,并设△OA1P1、△A1A2P2、△A2A3P3…面积分别为S1、S2、S3…,按此作法进行下去,则Sn的值为 (n为正整数).
 (x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5,并设其面积分别为S1、S2、S3、S4、S5,则S1+S2+S3+S4+S5的值为( )
(x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5,并设其面积分别为S1、S2、S3、S4、S5,则S1+S2+S3+S4+S5的值为( )