题目内容
【题目】如图,在平面直角坐标系中,将四边形ABCD称为“基本图形”,且各点的坐标分别为A(4,4),B(1,3),C(3,3),D(3,1).
①画出“基本图形”关于原点O对称的四边形A1B1C1D1 , 并填出A1 , B1 , C1 , D1的坐标;
②画出“基本图形”绕B点顺时针旋转90°所成的四边形A2B2C2D2
A1( , )B1( , )
C1( , )D1( , )
【答案】﹣4;﹣4;﹣1;﹣3;﹣3;﹣3;﹣3;﹣1
【解析】解:①根据已坐标系中点关于原点对称的坐标特点,即可得出答案:
A1(﹣4,﹣4),B1(﹣1,﹣3),
C1(﹣3,﹣3),D1(﹣3,﹣1);
②如图所示: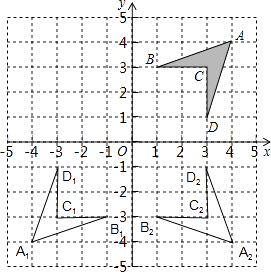
【考点精析】掌握关于原点对称的点的坐标是解答本题的根本,需要知道两个点关于原点对称时,它们的坐标的符号相反,即点P(x,y)关于原点的对称点为P’(-x,-y).

练习册系列答案
相关题目
【题目】七(1)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据整理如下表(部分):
月均用 水量x/m3 | 0< x≤5 | 5< x≤10 | 10< x≤15 | 15< x≤20 | x>20 |
频数/户数 | 12 | 20 | 3 | ||
百分比 | 12% | 7% |
若该小区有800户家庭,据此估计该小区月均用水量不超过10 m3的家庭有________户.