题目内容
【题目】如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2= ![]() (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则 ![]() = .
= . 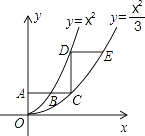
【答案】![]()
【解析】解:设A点坐标为(0,a),(a>0),
则x2=a,解得x= ![]() ,
,
∴点B( ![]() ,a),
,a), ![]() =a,
=a,
则x= ![]() a,
a,
∴点C( ![]() a,a),
a,a),
∴BC= ![]() a﹣
a﹣ ![]() .
.
∵CD∥y轴,
∴点D的横坐标与点C的横坐标相同,为 ![]() a,
a,
∴y1=( ![]() a)2=3a,
a)2=3a,
∴点D的坐标为( ![]() a,3a).
a,3a).
∵DE∥AC,
∴点E的纵坐标为3a,
∴ ![]() =3a,
=3a,
∴x=3 ![]() ,
,
∴点E的坐标为(3 ![]() ,3a),
,3a),
∴DE=3 ![]() ﹣
﹣ ![]() a,
a,
∴ ![]() =
= ![]() =
= ![]() .
.
故答案是: ![]() .
.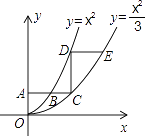
【考点精析】关于本题考查的二次函数的图象和二次函数的性质,需要了解二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能得出正确答案.

练习册系列答案
相关题目
【题目】受地震的影响,某超市鸡蛋供应紧张,需每天从外地调运鸡蛋1200斤.超市决定从甲、乙两大型养殖场调运鸡蛋,已知甲养殖场每天最多可调出800斤,乙养殖场每天最多可调出900斤,从两养殖场调运鸡蛋到超市的路程和运费如表:
到超市的路程(千米) | 运费(元/斤千米) | |
甲养殖场 | 200 | 0.012 |
乙养殖场 | 140 | 0.015 |
(1)若某天调运鸡蛋的总运费为2670元,则从甲、乙两养殖场各调运了多少斤鸡蛋?
(2)设从甲养殖场调运鸡蛋x斤,总运费为W元,试写出W与x的函数关系式,怎样安排调运方案才能使每天的总运费最省?