Question

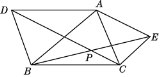
【题目】如图所示，在△ABC外作△ABD和△ACE，使AD＝AB，AE＝AC，且∠DAB＝∠EAC，连接BE，CD相交于P点，求证：点A在∠DPE的平分线上．

Answer 1

【答案】见解析

【解析】

如图，过A点作AM⊥CD于点M，作AN⊥BE于点N，先通过“边角边”证明△BAE≌△DAC，

得到BE＝DC，S△BAE＝S△DAC，然后通过三角形面积公式得到AN＝AM，即得证.

证明：如图，过A点作AM⊥CD于点M，作AN⊥BE于点N，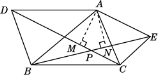

∵∠DAB＝∠EAC，

∴∠DAB＋∠BAC＝∠EAC＋∠BAC，即∠DAC＝∠BAE，

在△BAE和△DAC中，

，

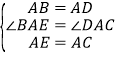∴△BAE≌△DAC（SAS），

∴BE＝DC，S△BAE＝S△DAC，

∵AM⊥CD，AN⊥BE，

∴BE·AN＝CD·AM，

∴AN＝AM，

∴点A在∠DPE的平分线上．