题目内容
【题目】如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,∠BCD=45°,将腰CD以点D为中心逆时针旋转90°至ED,连结AE,CE,则△ADE的面积是( ) 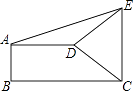
A.1
B.2
C.3
D.4
【答案】A
【解析】解:作DH⊥BC于H,EF⊥AD于F,如图,则四边形ABHD为矩形,
∴BH=AD=2,
∴CH=BC﹣BH=3﹣2=1,
∵腰CD以点D为中心逆时针旋转90°至ED,
∴DE=DC,∠EDC=90°,
∵∠EDF+∠CDF=90°,∠CDF+∠CDH=90°,
∴∠EDF=∠HDC,
在△EDF和△CDH中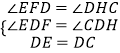 ,
,
∴△EDF≌△CDH,
∴EF=CH=1,
∴△ADE的面积= ![]() ×2×1=1.
×2×1=1.
故选A.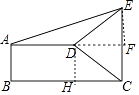
【考点精析】解答此题的关键在于理解直角梯形的相关知识,掌握一腰垂直于底的梯形是直角梯形,以及对旋转的性质的理解,了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

练习册系列答案
相关题目
【题目】为了解学生的体能情况,随机选取了1000名学生进行调查,并记录了他们对长跑、短跑、跳绳、跳远四个项目的喜欢情况,整理成以下统计表,其中“√”表示喜欢,“×”表示不喜欢.
项目 | 长跑 | 短跑 | 跳绳 | 跳远 |
200 | √ | × | √ | √ |
300 | × | √ | × | √ |
150 | √ | √ | √ | × |
200 | √ | × | √ | × |
150 | √ | × | × | × |
(1)估计学生同时喜欢短跑和跳绳的概率;
(2)估计学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率;
(3)如果学生喜欢长跑、则该同学同时喜欢短跑、跳绳、跳远中哪项的可能性大?