题目内容
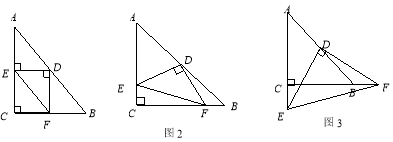
【题目】已知:Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D点旋转,它的两边分别交AC,CB(或它们的延长线)于E、F,当∠EDF绕D点旋转到DE⊥AC于E时(如图1),
(1)易证![]() +
+![]() =
=![]()
![]() .
.
![]() (2)当∠EDF绕
(2)当∠EDF绕![]() 点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,
点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,![]() 、
、![]() 、
、![]() 又有怎样的数量关系?请写出你的猜想,不需证明.
又有怎样的数量关系?请写出你的猜想,不需证明.
【答案】(1)答案见解析;(2)![]() -
-![]() =
=![]() .
.
【解析】
试题分析:(1)首先连接CD,得出△ECD和△FBD全等,根据△CDB的面积等于△ABC面积的一半进行说明;(2)根据第一题同样的思路得出三角形面积之间的关系.
试题解析:(1)在图2情况下,式子成立.证明如下:

连接CD∵AB=BC,D为AB边的中点 ∴CD⊥AB,∠ACD=∠BCD=45°, ![]()
∵∠ACB=90°,D为AB边的中点 ∴CD=BD=![]() AB ∠B=45°
AB ∠B=45°
∴∠B=∠ACD ∵∠EDC+∠CDF=90°,∠CDF+∠FDB=90° ∴∠EDC=∠FDB
∴△ECD≌△FBD ∴![]()
∵![]() =
=![]() =
=![]()
又![]() ∴
∴![]()
(2)在图3情况下,式子不成立.猜想:![]() -
-![]() =
=![]() .
.

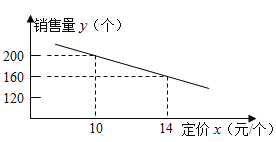
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第![]() (1≤
(1≤![]() ≤90)天的售价与销量的相关信息如下表:
≤90)天的售价与销量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200﹣2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为![]() 元.
元.
(1)求出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
【题目】春节将至,某移动公司计划推出两种新的计费方式,如下表所示:
方式1 | 方式2 | |
月租费 | 30元/月 | 0 |
本地通话费 | 0.20元/分钟 | 0.40元/分钟 |
请解决以下两个问题:(通话时间为正整数)
(1)若本地通话100分钟,按方式一需交费多少元?按方式二需交费多少元?
(2)对于某月本地通话,当通话多长时间时,按两种计费方式的收费一样多?