题目内容

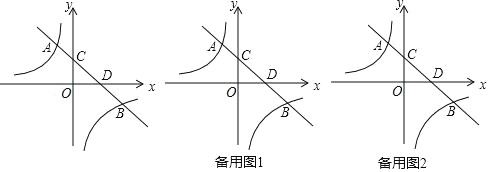
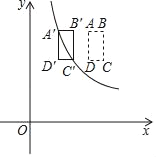
【题目】如图，在平面直角坐标系中，矩形ABCD的顶点A、C的坐标分别为（4，6）、（5，4），且AB平行于x轴，将矩形ABCD向左平移，得到矩形A′B′C′D′．若点A′、C′同时落在函数的图象上，则k的值为（　　）

A. 6 B. 8 C. 10 D. 12

【答案】D

【解析】

设点A′、C′的坐标分别为（4﹣a，6），（5﹣a，4），依据点A′、C′同时落在函数的图象上，可得方程6（4﹣a）＝4（5﹣a），求得a的值即可得到k的值．

解：∵点A、C的坐标分别为（4，6）、（5，4），且AB平行于x轴，

∴平移后，可设点A′、C′的坐标分别为（4﹣a，6），（5﹣a，4），

∵点A′、C′同时落在函数的图象上，

∴6（4﹣a）＝4（5﹣a），

解得a＝2，

∴C'（3，4），

∴k＝3×4＝12，

故选：D．

练习册系列答案
相关题目

【题目】已知正比例函数y＝k1x的图象与反比例函数的图象的一个交点是（1，3）．

（1）写出这两个函数的表达式，并确定这两个函数图象的另一个交点的坐标；

（2）画出草图，并据此写出使反比例函数大于正比例函数的x的取值范围．

【题目】如图，直线 y=﹣x+2 与反比例函数 y=（k≠0）的图象交于 A（a，3）、B（3，b）两点，直线 AB 交 y 轴于点 C、交 x 轴于点 D．

(1)请直接写出 a=_______，b=______，反比例函数的解析式为_______．

(2)在 x 轴上是否存在一点 E，使得∠EBD=∠OAC，若存在请求出点 E 的坐标， 若不存在，请说明理由．

(3)点P 是 x 轴上的动点，点 Q 是平面内的动点，是以 A、B、P、Q 为顶点的四边形是矩形，若存在请求出点 Q 的坐标，若不存在请说明理由．

【题目】如图，在△ABC中，AB＝5，AC＝3，BC＝4，将△ABC绕A逆时针方向旋转40°得到△ADE，点B经过的路径为弧BD，则图中阴影部分（△ABC以外的部分）的面积为_____．

【题目】如图，在△ABC 中，AB＝AC．D 是 BC 上一点，且 AD＝BD．将△ABD 绕点 A 逆时针旋转得到△ACE．

（1）求证：AE∥BC；

（2）连结 DE，判断四边形 ABDE 的形状，并说明理由．

【题目】△ABC是等腰直角三角形，∠ACB＝90°，AB＝8cm，动点P、Q以2cm/s的速度分别从点A、B同时出发，点P沿A到B向终点B运动，点Q沿B到A向终点A运动，过点P作PD⊥AC于点D，以PD为边向右侧作正方形PDEF，过点Q作QG⊥AB，交折线BC﹣CA于点G与点C不重合，以QG为边作等腰直角△QGH，且点G为直角顶点，点C、H始终在QG的同侧，设正方形PDEF与△QGH重叠部分图形的面积为S（cm2），点P运动的时间为t（s）（0＜t＜4）．

（1）当点F在边QH上时，求t的值．

（2）点正方形PDEF与△QGH重叠部分图形是四边形时，求S与t之间的函数关系式；

（3）当FH所在的直线平行或垂直AB时，直接写出t的值．

【题目】如图，在边长为5的菱形OABC中，sin∠AOC＝，O为坐标原点，A点在x轴的正半轴上，B，C两点都在第一象限．点P以每秒1个单位的速度沿O→A→B→C→O运动一周，设运动时间为t（秒）．请解答下列问题：

（1）当CP⊥OA时，求t的值；

（2）当t＜10时，求点P的坐标（结果用含t的代数式表示）；

（3）以点P为圆心，以OP为半径画圆，当⊙P与菱形OABC的一边所在直线相切时，请直接写出t的值．

【题目】如图，已知 A、B是线段MN上的两点，MN4，MA1，MB1．以A为中心顺 时针旋转点M，以B为中心逆时针旋转点N，使MN 两点重合成一点C，构成△ABC，设ABx.（1）则x的取值范围是_________；（2）△ABC的最大面积是_________.

C

【题目】如图，正方形的边长为，是边的中点，点在射线上，过作于，设．

（1）求证：；

（2）当也是边中点时，求的值；

（3）若以，，为顶点的三角形也与相似，试求的值；

（4）当点与点重合时，设交于点，试判断与的大小关系并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网