题目内容
【题目】如图,在边长为5的菱形OABC中,sin∠AOC=![]() ,O为坐标原点,A点在x轴的正半轴上,B,C两点都在第一象限.点P以每秒1个单位的速度沿O→A→B→C→O运动一周,设运动时间为t(秒).请解答下列问题:
,O为坐标原点,A点在x轴的正半轴上,B,C两点都在第一象限.点P以每秒1个单位的速度沿O→A→B→C→O运动一周,设运动时间为t(秒).请解答下列问题:
(1)当CP⊥OA时,求t的值;
(2)当t<10时,求点P的坐标(结果用含t的代数式表示);
(3)以点P为圆心,以OP为半径画圆,当⊙P与菱形OABC的一边所在直线相切时,请直接写出t的值.
【答案】(1)t=3;(2)P(![]() t+2,
t+2,![]() t﹣4);(3)t的值为
t﹣4);(3)t的值为![]() 秒或4秒或16秒或
秒或4秒或16秒或![]() 秒
秒
【解析】
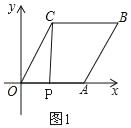
(1)如图1,过点C作CP⊥OA,交x轴于点P.就可以求出OP的值,由勾股定理就可以求出的OP值,进而求出结论;
(2)t<10时,P在OA或AB上运动,所以分两种情况:①当0≤t≤5时,如图1,点P在OA上,OP=t,可得P的坐标;②当5<t<10时,如图2,点P在AB上,构建直角三角形,根据三角函数定义可得P的坐标;
(3)设切点为G,连接PG,分⊙P与四边相切,其中P在AB和BC时,与各边都不相切,所以分两种情况:
①当P在OA上时,根据三角函数列式可得t的值;
②当P在OC上时,同理可得结论.
(1)如图1,
当CP⊥OA时,sin∠AO![]()
![]()
在Rt△OPC中,OC=5,PC=4,则OP=3,
∴![]()
(2)当0≤t≤5时,如图1,点P在OA上,
∴P(t,0);
当5<t<10时,如图2,点P在AB上,
过P作PH⊥x轴,垂足为H,
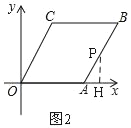
则∠AOC=∠PAH,
∴sin∠PAH=sin∠AO![]()
![]()
∴![]()
∴![]()
(3)设切点为G,连接PG,
分两种情况:
①当P在OA上时,如图3,
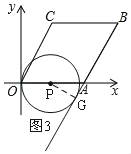
⊙P与直线AB相切,
∵OC∥AB,
∴∠AOC=∠OAG,
∴sin∠AOC=sin∠OA![]()
![]()
∴![]()
⊙P与BC相切时,如图4,

则PG=t=OP=4;
②当点P在OC上时,
⊙P与AB相切时,如图5,
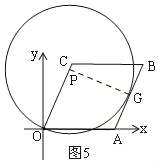
∴OP=PG=4,
∴4×5﹣t=4,
t=16,
⊙P与直线BC相切时,如图6,

∴PG⊥BC,
∵BC∥AO,
∴∠AOC=∠GCP,
∴sin∠AOC=sin∠GC![]()
∵OP=PG=20﹣t,
∴![]()
∴![]()
综上所述,t的值![]()

【题目】某公司欲招聘一名公务人员,对甲、乙两位应试者进行了面试和笔试,他们的成绩(百分制)如表所示:
应试者 | 面试 | 笔试 |
甲 | 86 | 90 |
乙 | 92 | 83 |
(1)如果公司认为面试和笔试同等重要,从他们的成绩看,谁将被录取?
(2)如果公司认为作为公务人员面试成绩应该比笔试成绩更重要,并分别赋予它们6和4的权,计算甲、乙两人各自的平均成绩,谁将被录取?