��Ŀ����
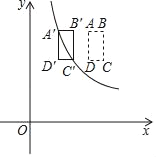
����Ŀ����ͼ��ֱ�� y=��x+2 �뷴�������� y=![]() ��k��0����ͼ���� A��a��3����B��3��b�����㣬ֱ�� AB �� y ���ڵ� C���� x ���ڵ� D��
��k��0����ͼ���� A��a��3����B��3��b�����㣬ֱ�� AB �� y ���ڵ� C���� x ���ڵ� D��
(1)��ֱ��д�� a=_______��b=______�������������Ľ���ʽΪ_______��
(2)�� x �����Ƿ����һ�� E��ʹ����EBD=��OAC��������������� E �����꣬ �������ڣ���˵�����ɣ�
(3)��P �� x ���ϵĶ��㣬�� Q ��ƽ���ڵĶ��㣬���� A��B��P��Q Ϊ������ı����Ǿ��Σ�������������� Q �����꣬����������˵�����ɣ�
���𰸡�(1)-1��-1��-3��(2)���������ĵ� E ����Ϊ��0��0����![]() ��0����(3)���������ĵ� Q ����Ϊ��0����4����0��4����1+
��0����(3)���������ĵ� Q ����Ϊ��0����4����0��4����1+![]() ��2����1��
��2����1��![]() ��2����
��2����
��������
��1�����ô���ϵ�������ɽ�����⣻
���������Σ��ٵ��� E �� O �غ�ʱ����EBD=��OAC����ʱ E��0��0�������� BE���OA�����E��BD=��OAC���ֱ���⼴�ɽ�����⣻
���������λ���ͼ�Σ��ֱ���⼴�ɽ�����⣻
(1)��A��a��3����B��3��b�������� y=��x+2 �ϣ�
��a=��1��b=��1��
��A����1��3������3����1����
��A����1��3���� y=![]() �ϣ�
�ϣ�
��k=��3��
�ʴ�Ϊ��1����1����3��
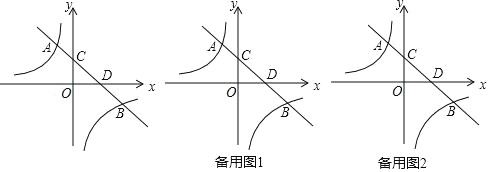
��ͼ 1 �У����� OB��
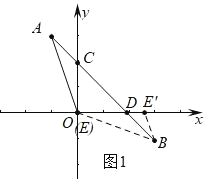
��A����1��3����B��3����1����
��OA=OB= ![]() ��
��
���OAC=��OBD��
������ E �� O �غ�ʱ����EBD=��OAC����ʱ E��0��0������ BE���OA������E��BD=��OAC��
������ D��2��0����
��AD= ![]() =3
=3![]() ��BD=
��BD= ![]() =
= ![]() ��
��
�� BE���OA��
��![]()
�� ![]() ��
��
��DE��=![]()
��OE��= ![]() ��
��
��E�䣨![]() ��0����
��0����
�������������������ĵ� E ����Ϊ��0��0����![]() ��0����
��0����
���ڣ���ͼ 2 �У�
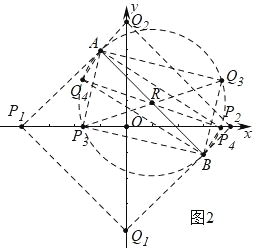
�����ı��� AP1Q1B �Ǿ���ʱ����֪ P1����4��0����
�� B��3����1������ƽ�� 3 ����λ������ƽ�� 3 ����λ�õ� Q1��0����4����
�����ı��� BP2Q2A �Ǿ���ʱ��P2��4��0����
�� A��3����1������ƽ��һ����λ������ƽ��һ����λ�õ� Q2��0��4����
���� AB �Ǿ��εĶԽ���ʱ���� AB ���е�Ϊ R��1��1������ P3��m��0����
��RP=2![]() ��
��
�ࣨ1��m��2+12=��2![]() ��2��
��2��
�� m=1+![]() �� 1��
�� 1��![]() ��
��
��P3��1��![]() ��0����P4��1+
��0����P4��1+![]() ��2����
��2����
��Q3��1+![]() ��2����Q4��1��
��2����Q4��1��![]() ��2����
��2����
�������������������ĵ� Q ����Ϊ��0����4����0��4����1+![]() ��2����1-
��2����1-![]() ��2����
��2����

����Ŀ��ij��˾����Ƹһ��������Ա���Լס�����λӦ���߽��������Ժͱ��ԣ����ǵijɼ����ٷ��ƣ������ʾ��
Ӧ���� | ���� | ���� |
�� | 86 | 90 |
�� | 92 | 83 |
��1�������˾��Ϊ���Ժͱ���ͬ����Ҫ�������ǵijɼ�����˭����¼ȡ��
��2�������˾��Ϊ��Ϊ������Ա���Գɼ�Ӧ�ñȱ��Գɼ�����Ҫ�����ֱ�������6��4��Ȩ������ס������˸��Ե�ƽ���ɼ���˭����¼ȡ��