��Ŀ����
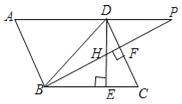
����Ŀ����ABC�ǵ���ֱ�������Σ���ACB��90�㣬AB��8cm������P��Q��2cm/s���ٶȷֱ�ӵ�A��Bͬʱ��������P��A��B���յ�B�˶�����Q��B��A���յ�A�˶�������P��PD��AC�ڵ�D����PDΪ�����Ҳ���������PDEF������Q��QG��AB��������BC��CA�ڵ�G���C���غϣ���QGΪ��������ֱ�ǡ�QGH���ҵ�GΪֱ�Ƕ��㣬��C��Hʼ����QG��ͬ�࣬��������PDEF���QGH�ص�����ͼ�ε����ΪS��cm2������P�˶���ʱ��Ϊt��s����0��t��4����
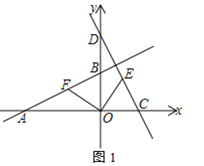
��1������F�ڱ�QH��ʱ����t��ֵ��
��2����������PDEF���QGH�ص�����ͼ�����ı���ʱ����S��t֮��ĺ�����ϵʽ��
��3����FH���ڵ�ֱ��ƽ�л�ֱABʱ��ֱ��д��t��ֵ��
���𰸡���1��t��![]() s;��2��������;��3��t��
s;��2��������;��3��t��![]() s��
s��![]() s��
s��![]() s��
s��
��������
��1����ͼ1�У�����F�ڱ�QH��ʱ����֪AP��PQ��BQ�����AB�ij����ɽ�����⣻
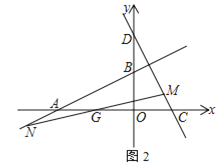
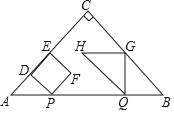
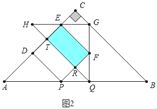
��2��������������ͼ2�У�����F��GQ��ʱ����֪AP��BQ��2t��PD��PF��![]() t��PQ��QF��t���г����̼��ɽ�����⣻����ͼ3�У��ص��������ı���GHRTʱ��
t��PQ��QF��t���г����̼��ɽ�����⣻����ͼ3�У��ص��������ı���GHRTʱ��
��3��������������������ͼ5�У���FH��ABʱ���ӳ�HF��AB��T����֪AP��BQ��GQ��HG��TQ��2t��PT��t������ͼ7�У���FH��ABʱ���ֱ��г����̼��ɽ�����⣮����ͼ8�У���HF��ABʱ��
�⣺��1����ͼ1�У�����F�ڱ�QH��ʱ����֪AP��PQ��BQ��
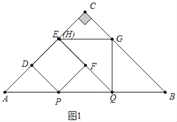
��Rt��ABC��AB��8��
��t![]() sʱ����F�ڱ�QH�ϣ�
sʱ����F�ڱ�QH�ϣ�
��2����ͼ2�У�����F��GQ��ʱ����֪AP=BQ=2t��PD=PF=![]() t��PQ=PF=t��
t��PQ=PF=t��
��2t+t+2t��8��
��t![]() ��
��
�ɣ�1����֪����![]() ʱ��������PDEF����QGH�ص�����ͼ�����ı���
ʱ��������PDEF����QGH�ص�����ͼ�����ı���
��ʱ![]()
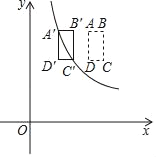
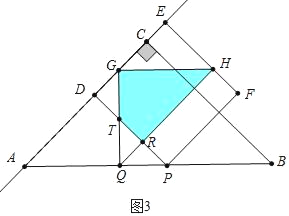
��ͼ3�У���H��EF��ʱ������![]()
���t![]() ��
��
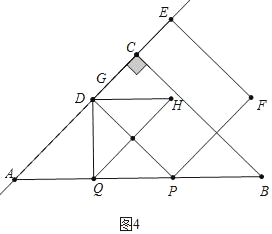
��ͼ4�У���G��D�غ�ʱ����֪4t��8��t�����t![]() ��
��
��![]() ʱ��
ʱ��![]()
��3������ͼ5�У���FH��ABʱ���ӳ�HF��AB��T����֪AP��BQ��GQ��HG��TQ��2t��PT��t��
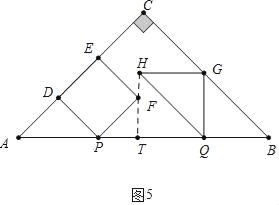
��6t+t��8��
��t=![]() ��
��
����ͼ7�У���HF��AB��Tʱ��
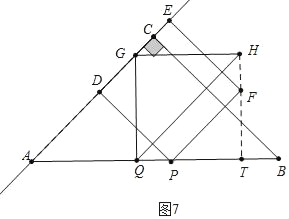
��TB��8��2��8��2t����8��3t�����t=![]() ��
��
����ͼ8�У���HF��ABʱ����t+2t��8��
��t=![]() ��
��
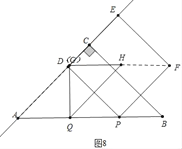
����������t=![]() s��
s��![]() s��
s��![]() sʱ��FH���ڵ�ֱ��ƽ�л�ֱ��AB��
sʱ��FH���ڵ�ֱ��ƽ�л�ֱ��AB��

 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�