题目内容
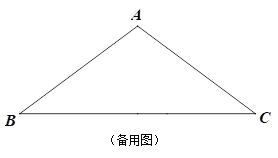
【题目】如图，AB∥CD，AE、DE分别平分∠BAD和∠ADC，求证：AD=AB+CD。
【答案】见解析.
【解析】
延长DE交AB的延长线于H．首先证明AE⊥DH，然后证明ED＝EH，△CED≌△BEH，可得CD＝BH，由此即可解决问题．
证明：延长DE交AB的延长线于H．
∵AB∥CD，AE、DE分别平分∠BAD和∠ADC，
∴∠ADC＋∠DAB＝180°，∠CDE＝∠H＝∠ADE，∠DAE＝
∠DAB，
∠ADE＝∠ADC，
∴∠DAE＋∠ADE＝90°，AD= AH，
∴∠AED＝90°，
∴AE⊥DH，
∴ED＝EH，
在△CED和△BEH中，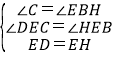
，
∴△CED≌△BEH(AAS)，
∴CD＝BH，
∴AD= AH =AB＋BH＝AB＋CD．
练习册系列答案
名校课堂系列答案
相关题目
【题目】某垃圾处理厂，对不可回收垃圾的处理费用为90元/吨，可回收垃圾的分拣处理费用也为90元/吨，分拣后再被相关企业回收，回收价格如下表：
垃圾种类 | 纸类 | 塑料类 | 金属类 | 玻璃类 |
回收单价（元/吨） | 500 | 800 | 500 | 200 |
据了解，可回收垃圾占垃圾总量的60%，现有
三个小区12月份产生的垃圾总量分别为100吨,100吨和
吨.
(1)已知
小区金属类垃圾质量是塑料类的5倍，纸类垃圾质量是塑料类的2倍.设塑料类的质量为
吨，则小区可回收垃圾有______吨，其中玻璃类垃圾有_____吨(用含的代数式表示)
(2)
小区纸类与金属类垃圾总量为35吨，当月可回收垃圾回收总金额扣除所有垃圾处理费后，收益16500元.求12月份该小区可回收垃圾中塑料类垃圾的质量.
(3)
小区发现塑料类与玻璃类垃圾的回收总额恰好相等,所有可回收垃圾的回收总金额为12000元.设该小区塑料类垃圾质量为
吨，求与的数量关系.
