Question

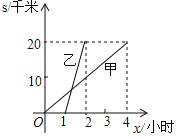
【题目】通过电脑拨号上“因特网”的费用是由电话费和上网费两部分组成，过去，某市网民通过电脑拨号上“因特网”的费用为电话费每3分钟0.18元，上网费每小时7.2元，现在，该市对上“因特网”的费用作了调整：电话费每3分钟0.22元，上网费为每月不超过60小时，按每小时4元计算；超过60小时部分，按每小时8元计算.

（1）根据调整后的规定，用解析式表示网民每月上“因特网”的费用（元）与上网时间之间的函数关系式；

（2）资费调整前，网民小刚在其家庭经济预算中，一直有一笔每月70小时的上网费用支出，因“因特网”资费调整后，小刚要想不超过其家庭经济预算中的上网费用支出，他现在每月至多可上网多少小时？

（3）从资费调整前后该市网民上网费用的支出增减情况分析，哪些网民支出增加？哪些网民支出减少？

Answer 1

【答案】（1）y= ；（2）至多可上网约80.32h；（3）当上网时间小于150时,调整后需费用少;当等于150时,调整前后所需费用相同;当大于150时,调整前所需费用少.

【解析】

（1）对于第一问,根据已知调整后“因特网”的费用调整为电话0.22元/3min,上网费为每月不超过60h,按4元/h计算;可以得出调整后的电话费为0.22*20=4.4(元/时）;再结合上网费用=网费电话费,网费不超过60h,为4元/h,即每小时上网所花费用8.4,网费超过60h,为8元/h,即超时每小时为12.4,即可解答;

（2）由已知条件网民晓刚在其家庭经济预算中,一直有一笔每月70h的上网费用支出,可以得出上网70h所需的费用为(3.6+7.2)×70=756(元);资费调整后,若上网60h,则所需费用为8.4×60=504(元,因为756＞504,所以晓刚现在上网时间超过60h,得出关系式12.4(x-60)+504≤756,即可解答.

（3）先设出未知数调整前所需费用y 元,调整后所需费用为y 元,然后分情况讨论,得出解答结果.

(1)由题意知调整后每小时的电话费为：0.22×20=4.4(元/时)

根据上网费用=网费电话费,网费不超过60h,为4元/h,即每小时上网所花费用8.4元

若网费,超过60h,为8元/h,即超时时每小时的上网费用为12.4元

所以设上网时间为x,与费用y的函数关系式为

y=

(2)资费调整前,上网70h所需的费用为(3.6+7.2)×70=756(元)

资费调整后,若上网60h,则所需费用为：8.4×60=504(元)

因为756＞504，

所以晓刚现在上网时间超过60h，

由12.4(x-60)+504≤756，

解得：x≤80.32h.

所以小刚现在每月至多可上网约80.32h.

(3)设调整前所需费用y元,调整后所需费用为y元.则y=10.8x

当0≤x≤60时，

y=8.4x，

由10.8x＞8.4x，

故y＞y，

当x＞60,y=12.4x240，

当y=y时，

10.8x=12.4x-240，

解得：x=150，

当y＞y时，

10.8x＞12.4x-240，

解得：x＜150，

当y＜y时，

10.8x＜12.4x-240，

解得：x＞150，

当上网时间小于150时,调整后需费用少;

当等于150时,调整前后所需费用相同;

当大于150时,调整前所需费用少.