Question

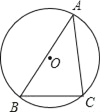
【题目】如图，已知在中，，，是边上一点，以为圆心，为半径的⊙与边的另一个交点为，连结、．

（1）求△ABC的面积；

（2）设，的面积为，求关于的函数关系式，并写出自变量的取值范围；

（3）如果是直角三角形，求的长．

Answer 1

【答案】（1）12（2） （3）或

【解析】分析：(1)分别求出BC和BC上的高；(2)作DM⊥AB垂足为M，用含x的式子表示出AP和DM；(3)分∠ADP＝90°和∠PAD＝90°两种情况求解.

详解：(1)∵AB＝AC＝5，cosB＝，

∴BC＝8，BC上的高为3，

∴S△ABC＝×8×3＝12.

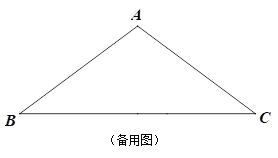
(2)如图，作DM⊥AB垂足为M，

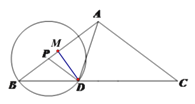
∵PB＝x，cosB＝，得BD＝，∴DM＝×.

又∵AB＝5，PB＝x，∴AP＝5－x.

∴y＝AP·DM＝(5－x)×.

∴.

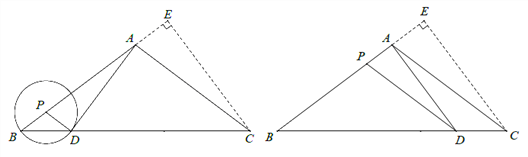
(3)∠APD＜90°，

过C作CE⊥AB交BA的延长线于E，可得cos∠CAE＝.

①当∠ADP＝90°时，

cos∠APD＝cos∠CAE＝，则，解得x＝；

②当∠PAD＝90°时，，解得x＝.

所以PB的值为或.