Question

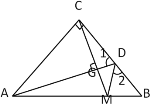
【题目】△ABC中，AC=BC，∠ACB=90°，CD=BD，∠1=∠2，求证：CM⊥AD。

Answer 1

【答案】见解析.

【解析】

过点C作CE⊥AB交AB于点E，交AD于点F，AD与CM交于点G，根据∠B=∠BCE=45°，CD=BD，∠1=∠2证明△CDF≌△BDM，得到CF=BM，然后再由AC=BC及通过SAS证明△ACF≌△CBM，得到∠CAF=∠BCM，再根据角之间的等量代换可证明∠CFG+∠ECM=90°，问题得证.

证明：过点C作CE⊥AB交AB于点E，交AD于点F，AD与CM交于点G，

∵AC=BC，∠ACB=90°，

∴∠B=∠BCE=45°，

在△CDF和△BDM中，，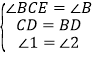

∴△CDF≌△BDM（ASA），

∴CF=BM，

在△ACF和△CBM中，，

∴△ACF≌△CBM（SAS），

∴∠CAF=∠BCM，

∵∠BCM +∠ECM =∠CAF+∠EAF=45°，

∴∠ECM =∠EAF，

∵∠AFE=∠CFG，且∠AFE+∠EAF=90°，

∴∠CFG+∠ECM=90°，即∠CGF=90°，

∴CM⊥AD.