题目内容
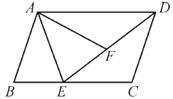
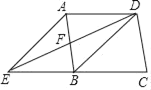
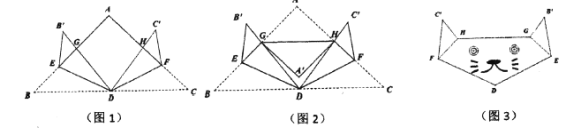
【题目】如图1,在面积为![]() 的等腰
的等腰![]() 纸板中,在直角边
纸板中,在直角边![]() ,
,![]() 上各取一点
上各取一点![]() ,
,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() ,
,![]() 分别沿
分别沿![]() ,
,![]() 折叠,对应边
折叠,对应边![]() ,
,![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,再将
,再将![]() 沿
沿![]() 折叠,点
折叠,点![]() 的对应点
的对应点![]() 落在
落在![]() 的内部(如图2所示),翻面画上眼睛和鼻子,得到了一幅可爱的“猫脸图”(如图3所示),若点
的内部(如图2所示),翻面画上眼睛和鼻子,得到了一幅可爱的“猫脸图”(如图3所示),若点![]() 与点
与点![]() 之间的距离为
之间的距离为![]() ,则五边形
,则五边形![]() 的面积为__________
的面积为__________![]() .
.
【答案】![]()
【解析】
连接AD和GH交于点O, B′C′与AD交于点R、GH、,过点H作 HM⊥BC于点M,过点F作 FN⊥BC于点N,由对称性可知,点A′在AD上,∵∠C=45°,∴△HMC、△FNC是等腰直角三角形,因为等腰RtΔABC面积为49cm2,可得AB=AC=7![]() ,AD=BD=DC=7,
,AD=BD=DC=7,
由B′C′=![]() ,得C′R =
,得C′R =![]() ,再由DC′=DC=7,由勾股定理得DR=
,再由DC′=DC=7,由勾股定理得DR=![]() ,所以C′R:RD:C′D=
,所以C′R:RD:C′D=![]() :
:![]() :7=3:4:5,易得△DHO∽△D C′R,所以HO:OD:DH= C′R:RD:C′D=3:4:5,
:7=3:4:5,易得△DHO∽△D C′R,所以HO:OD:DH= C′R:RD:C′D=3:4:5,
设HO=3a,OD=4a,DH=5a,易得四边形ODMH是矩形,△HMC、△FNC是等腰直角三角形,所以DM=OH=3a,HM=OD=MC=4a,而DM+MC=7a=7,解得a=1,即HM=OD=MC=4a=4,DH=5,DM=OH=3a=3,
由折叠得∠1=∠2,所以DH:DC=HF:FC=5:7,又因为FN∥HM,所以HF:FC=MN:NC=5:7,MC:NC=12:7即NC=![]() MC=
MC=![]() ×4=
×4=![]() =NF,再根据五边形GHFDE的面积=梯形GHCB -2S△DFC即可解答.
=NF,再根据五边形GHFDE的面积=梯形GHCB -2S△DFC即可解答.
连接AD和GH交于点O, B′C′与AD交于点R、GH、,过点H作 HM⊥BC于点M,过点F作 FN⊥BC于点N,
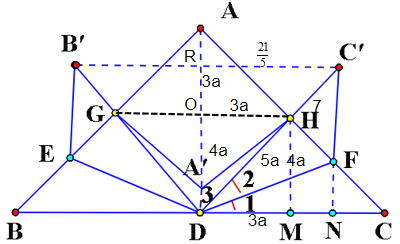
由对称性可知,点A′在AD上,∵∠C=45°,∴△HMC、△FNC是等腰直角三角形,
∵等腰RtΔABC面积为49cm2,∴AB=AC=7![]() ,AD=BD=DC=7,
,AD=BD=DC=7,
∵B′C′=![]() ,∴C′R =
,∴C′R =![]() ,
,
∵DC′=DC=7,∴由勾股定理得DR=![]() ,
,
∴C′R:RD:C′D=![]() :
:![]() :7=3:4:5,
:7=3:4:5,
∵易得△DHO∽△D C′R
∴HO:OD:DH= C′R:RD:C′D=3:4:5,
设HO=3a,OD=4a,DH=5a,
∵四边形ODMH是矩形,△HMC、△FNC是等腰直角三角形,
∴DM=OH=3a,HM=OD=MC=4a,
∵DM+MC=7a=7,∴a=1,即HM=OD=MC=4a=4,DH=5,DM=OH=3a=3,
∵∠1=∠2,
∴DH:DC=HF:FC=5:7,
又∵FN∥HM,
∴HF:FC=MN:NC=5:7,
∴MC:NC=12:7即NC=![]() MC=
MC=![]() ×4=
×4=![]() =NF,
=NF,
∴五边形GHFDE的面积=梯形GHCB -2S△DFC=![]() (6+14)×4-2×
(6+14)×4-2×![]() ×7×
×7×![]() =40-
=40-![]() =
=![]() .
.
故答案为:![]() .
.

【题目】为了参加2018年的全国初中生数学竞赛,乔老师利用寒假把甲、乙两名同学的前五个学期的数学成绩(单位:分)统计成下表:
第一学期 | 第二学期 | 第三学期 | 第四学期 | 第五学期 | |
甲 | 75 | 80 | 85 | 90 | 95 |
乙 | 95 | 87 | 88 | 80 | 75 |
(1)分别求出甲、乙两名同学前五个学期的数学平均成绩;
(2)在图中分别画出甲、乙两名同学前五个学期的数学成绩的折线统计图;
(3)如果你是乔老师,你认为应该派哪名学生参加数学竞赛?请简要说明理由.

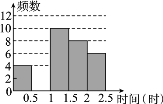
【题目】某中学对本校初中学生完成家庭作业的时间做了总量控制,规定学生每天完成家庭作业的时间少于1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间作了一次随机抽样调查,并绘制出频数分布表和频数分布直方图的一部分.
时间(时) | 频数 | 频率 |
0≤t<0.5 | 4 | 0.1 |
0.5≤t<1 | a | 0.3 |
1≤t<1.5 | 10 | 0.25 |
1.5≤t<2 | 8 | b |
2≤t<2.5 | 6 | 0.15 |
合计 | 1 |
(1)在频数分布表中,a=________,b=________;
(2)补全频数分布直方图;
(3)请估计该校1400名初中学生中,有多少名学生在1.5小时以内(不包括1.5小时)完成了家庭作业?![]()