题目内容
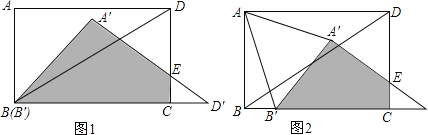
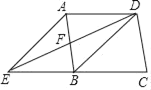
【题目】如图,在平行四边形ABCD中,DB=DA,∠ADB的角平分线与AB相交于点F,与CB的延长线相交于点E连接AE.
(1)求证:四边形AEBD是菱形.
(2)若四边形ABCD是菱形,DC=10,则菱形AEBD的面积是 .(直接填空,不必证明)
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由角平分线的性质和平行线的性质可得∠BED=∠BDE,可得BE=BD,即可证四边形AEBD是平行四边形,且DB=DA,可得结论;
(2)由菱形的性质可得AD=AB=10=DB,AB⊥DE,由等边三角形的性质和直角三角形性质可得AF=5,DF=![]() ,即可求菱形AEBD的面积.
,即可求菱形AEBD的面积.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADE=∠DEB,
∵DE平分∠ADB,
∴∠ADE=∠BDE,
∴∠BED=∠BDE,
∴BE=BD,且BD=DA,
∴AD=BE,且AD∥BE,
∴四边形ADBE是平行四边形,且AD=BD
∴四边形AEBD是菱形;
(2)∵四边形ABCD是菱形,
∴AB=AD=CD=10,且AD=BD,
∴△ABD是等边三角形,
∴∠BAD=60°,
∵四边形AEBD是菱形,
∴AF=BF,AB⊥DE,EF=DF,
∴∠ADF=30°,
∴AF=5,DF=5![]() ,
,
∴DE=10![]() ,
,
∴菱形AEBD的面积=![]() ×10×10
×10×10![]() =50
=50![]() ,
,
故答案为:50![]() .
.

 名校课堂系列答案
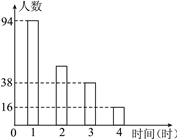
名校课堂系列答案【题目】发散思维2017·丰台区二模为了解某校八年级学生每周上网的时间,两名学生进行了抽样调查,小丽调查了八年级电脑爱好者中40名学生每周上网的时间,小杰从全校400名八年级学生中随机抽取了40名学生,调查了他们每周上网的时间.小丽与小杰整理各自的样本数据,如下表所示:
时间段(时/周) | 小丽抽样人数 | 小杰抽样人数 |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(表中每组数据包含最小值,不包含最大值)
(1)你认为哪名同学抽取的样本不合理?请说明理由;
(2)专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间,估计该校全体八年级学生中有多少名学生应适当减少上网的时间.