题目内容
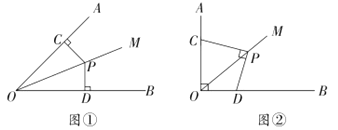
【题目】已如两个全等的等腰△ABC、△DEF,其中∠ACB=∠DFE=90°,E为AB中点,△DEF可绕顶点E旋转,线段DE,EF分别交线段CA,CB(或它们所在的直线)于M、N.
(1)如图1,当线段EF经过△ABC的顶点时,点N与点C重合,线段DE交AC于M,已知AC=BC=5,则MC= ;
(2)如果2,当线段EF与线段BC边交于N点,线段DE与线段AC交于M点,连MN,EC,请探究AM,MN,CN之间的等量关系,并说明理由;
(3)如图3,当线段EF与BC延长线交于N点,线段DE与线段AC交于M点,连MN,EC,则(2)中AM,MN,CN之间的等量关系还成立吗?请说明理由.

【答案】(1)![]() ;(2)见解析;(3)见解析
;(2)见解析;(3)见解析
【解析】
(1)根据AC=BC,E为AB中点,得出CE⊥AB,∠ACE=∠BCE=![]() ∠ACB=45°,∠A=∠ACE=45°,AE=CE,再根据DF=EF,∠DFE=90°,得出∠FED=45°,∠FED=
∠ACB=45°,∠A=∠ACE=45°,AE=CE,再根据DF=EF,∠DFE=90°,得出∠FED=45°,∠FED=![]() ∠AEC,即可得出AM=MC;
∠AEC,即可得出AM=MC;
(2)先在AM截取AH,使得AH=CN,连接EH,根据AE=CE,∠A=∠BCE=45°证出△AHE≌△CNE,HE=NE,∠AEH=∠CEN,∠HEM=∠AEC﹣∠AEH﹣MEC=∠AEC﹣∠CEN﹣MEC=∠AEC﹣∠MEF=90°﹣45°=45°,∠HEM=∠NEM=45°然后证出△HEM≌△NEM,HM=MN,最后根据AM=AH+HM=CN+MN即可得出答案;
(3)先在CB上截取CH=AM,根据SAS证得△AEM≌△CEH,得出EM=EH,∠AEM=∠CEH,AM=CH,再根据∠MEN和∠AEC的度数,得出∠CEH+∠CEN=∠HEN=45°,再在△EMN和△EHN中,根据SAS证得△EMN≌△EHN,得出MN=HN,即可求出答案.
解:(1)∵AC=BC,E为AB中点,
∴CE⊥AB,∠ACE=∠BCE=![]() ∠ACB=45°,
∠ACB=45°,
∴∠A=∠ACE=45°,
∴∠AEC=90°,AE=CE,
∵DF=EF,∠DFE=90°,
∴∠FED=45°,
∴∠FED=![]() ∠AEC,
∠AEC,
又∵AE=CE,
∴AM=MC=![]() AC=
AC=![]() ,
,
故答案为:![]() ;
;
(2)AM=MN+CN,理由如下:
如图2,在AM截取AH,使得AH=CN,连接EH,
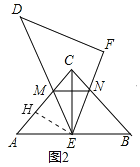
由(1)知AE=CE,∠A=∠BCE=45°
∵在△AHE与△CNE中:
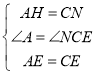 ,
,
∴△AHE≌△CNE(SAS),
∴HE=NE,∠AEH=∠CEN,
∴∠HEM=∠AEC﹣∠AEH﹣MEC=∠AEC﹣∠CEN﹣MEC=∠AEC﹣∠MEF=90°﹣45°=45°,
∴∠HEM=∠NEM=45
∵在△HEM与△NEM中:
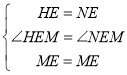 ,
,
∴△HEM≌△NEM(SAS),
∴HM=MN,
∴AM=AH+HM=CN+MN,
即AM=MN+CN;
(3)猜得:MN=AM+CN,理由如下:
如图3,在CB上截取CH=AM,连接EH,
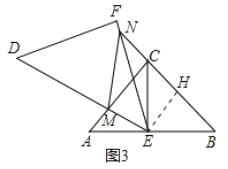
在△AEM和△CEH中,
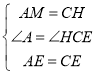 ,
,
∴△AEM≌△CEH(SAS),
∴EM=EH,∠AEM=∠CEH,AM=CH,
∵∠MEN=45°,∠AEC=90°,
∴∠AEM+∠CEN=45°,
∴∠CEH+∠CEN=∠HEN=45°,
∵∠MEN=∠HEN,
在△EMN和△EHN中,
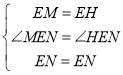 ,
,
∴△EMN≌△EHN(SAS),
∴MN=HN,
∴MN=CH+CN,
∴MN=AM+CN.

 口算能手系列答案
口算能手系列答案